13 Taylorin polynomi; funktioiden approksimoinnista
13.1 Taylorin polynomi
Tehtävä 552
Muodosta funktion f(x) = x4 + 3x3 + x2 + 2x + 8 kaikki Taylorin polynomit Tk (x, -2), k = 0, 1, 2, . . . (jolloin siis potenssien kantalukuna on x + 2). Kehitä ne myös siten, että kantalukuna on x. Piirrä polynomien kuvaajat ja vertaa niitä funktion kuvaajaan.Tehtävä 553
Etsi toisen asteen Taylorin polynomi ja vastaava jäännöstermi integraali- ja Lagrangen muodossa, kun funktiona on f ja kehityskeskuksena a:
a) f(x) = ex, a = -1, b) f(x) = 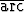 sin x, a =
sin x, a =  .
.
Tehtävä 554
Muodosta funktion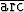 sin x astetta 10 oleva Taylorin polynomi a) pisteessä
x = 0, b) pisteessä x =
sin x astetta 10 oleva Taylorin polynomi a) pisteessä
x = 0, b) pisteessä x =  .
.
Tehtävä 555
Laske funktion f(x) = Taylorin polynomi T3(x, 2) ja piirrä funktion,
Taylorin polynomin sekä vastaavan jäännöstermin kuvaajat.
Taylorin polynomi T3(x, 2) ja piirrä funktion,
Taylorin polynomin sekä vastaavan jäännöstermin kuvaajat.
Tehtävä 556
Muodosta viidennen asteen Taylorin polynomi kehityskeskuksena origo funktiolle
f(x) =  .
.
Tehtävä 557
Olkoon f astetta 4 oleva polynomi, f(2) = -1, f'(2) = 0, f''(2) = 2, f''' (2) = -12, f(4)(2) = 24. Laske f(-1), f'(0) ja f''(1) mahdollisimman yksinkertaisesti.Tehtävä 558
Osoita, että parillisen (vastaavasti parittoman) funktion Maclaurinin polynomi sisältää vain muuttujan parillisia (parittomia) potensseja.Tehtävä 559
Todista, että ln(1 - 2x) < T3(x, 0), kun T3 tarkoittaa funktion ln(1 - 2x) Taylorin polynomia ja tarkastellaan arvoja x < , x
, x 0.
0.
Tehtävä 560
Todista:
1 - 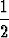 x2 +
x2 +  x4 > cos x > 1 -
x4 > cos x > 1 -  x2, kun x
x2, kun x  [-
[- ,
, 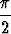 ].
].
Pitääkö epäyhtälöketju paikkansa välin ulkopuolella?
Tehtävä 561
Muodosta geometrisen summan kaavaa käyttäen funktiolle f(x) = (1 + x2)-1 Maclaurinin polynomi Tn(x, 0) indeksin n funktiona. Laske tämän avulla f(n)(0).Tehtävä 562
Muodosta funktion ln(1 + x) Maclaurinin polynomi Tn(x, 0) tarkastelemalla ensin funktion derivaattaa ja käyttämällä geometrisen summan kaavaa.Tehtävä 563
Olkoon f(x) = x3 ln(2 + x2). Määritä f(87)(0).Tehtävä 564
Olkoon funktion f toinen derivaatta f'' jatkuva välillä [a, a + h], jolloin
f(a + h) = f(a) + f'(a)h +  f''(a +
f''(a +  h)h2,
h)h2,
missä 
 [0, 1]. Osoita, että
[0, 1]. Osoita, että 
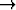
 , kun h
, kun h 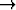 0, jos lisäksi f''' jatkuva ja f'''(a)
0, jos lisäksi f''' jatkuva ja f'''(a)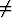 0.
0.
13.2 Taylorin polynomin sovellutuksia
Tehtävä 565
Millä tarkkuudella Taylorin polynomi T2(x, 0) antaa funktion f(x) arvot välillä [- ,
,  ], kun f(x) on
], kun f(x) on
a)  , b) cos x, c) tan x, d) esin x.
, b) cos x, c) tan x, d) esin x.
Tehtävä 566
Muodosta funktion f(x) = Maclaurinin polynomi T3(x, 0) ja arvioi
erotuksen f(x) - T3(x, 0) itseisarvoa. Mikä on tämän yläraja, kun |x| < 4?
Maclaurinin polynomi T3(x, 0) ja arvioi
erotuksen f(x) - T3(x, 0) itseisarvoa. Mikä on tämän yläraja, kun |x| < 4?
Tehtävä 567
Tutki, millä tarkkuudella funktion sin x arvot voidaan laskea Maclaurinin polynomin T5 (x, 0) avulla a) välillä [-1, 1], b) välillä [- ,
,  ].
].
Tehtävä 568
Tutki, millä tarkkuudella Maclaurinin polynomi x -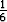 x3 antaa sinifunktion
arvot kulmille, jotka ovat välillä [0o, 10o].
x3 antaa sinifunktion
arvot kulmille, jotka ovat välillä [0o, 10o].
Tehtävä 569
Montako termiä funktion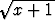 Maclaurinin polynomiin on otettava, jotta
välillä [
Maclaurinin polynomiin on otettava, jotta
välillä [ , 2] olevien lukujen neliöjuuret saataisiin lasketuksi viiden desimaalin
tarkkuudella?
, 2] olevien lukujen neliöjuuret saataisiin lasketuksi viiden desimaalin
tarkkuudella?
Tehtävä 570
Muodosta funktiolle cos x sellainen Maclaurinin polynomi, joka approksimoi funktiota välillä [-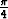 ,
,  ] tarkkuudella 10-4.
] tarkkuudella 10-4.
Tehtävä 571
Ilmoita jokin väli, jolla T2(x, 0) approksimoi funktiota cos x tarkkuudella 10-5 .Tehtävä 572
Millä tarkkuudella on

![[ ]
1 V~ -------
V~ -----2- 1- x2
1 + x](kuvat/ra1512x.gif)
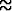
 ,
,
kun |x| < 0.15?
Tehtävä 573
Laske likiarvo luvulle 1/ approksimaatiokaavasta
approksimaatiokaavasta
ex 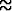 1 + x +
1 + x + 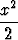 .
.
Arvioi virheen suuruutta ja merkkiä.
Tehtävä 574
Laske sopivaa Taylorin polynomia sekä neljää peruslaskutoimitusta käyttäen likiarvot seuraaville luvuille: a) 1/e tarkkuudella 10-4; b) sin 1o tarkkuudella 10-5; c) cos 10o tarkkuudella 10-3.Tehtävä 575
Määritä funktion sinh x - sin x ääriarvot.Tehtävä 576
Tutki, onko funktiolla
f(x) = 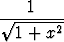 - 1 +
- 1 + 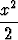
ääriarvoa kohdassa x = 0.
Tehtävä 577
Todista, että arvoilla x 0 pätee cos x - cosh x + x2 < 0.
0 pätee cos x - cosh x + x2 < 0.
Tehtävä 578
Määritä raja-arvo
limx 0
0
muodostamalla vastaava Maclaurinin polynomi.
Tehtävä 579
Käyrillä y = f(x) ja y = g(x) sanotaan olevan pisteessä x (vähintään) kertalukua n oleva kosketus, jos funktioiden arvot ja niiden derivaattojen arvot kertalukuun n saakka yhtyvät tässä pisteessä. Määritä käyrälle +
+  = 2
= 2 (a > 0)
kaarevuusympyrä pisteessä (a, a) ja osoita, että kosketuksen kertaluku on 3 (mutta ei
suurempi).
(a > 0)
kaarevuusympyrä pisteessä (a, a) ja osoita, että kosketuksen kertaluku on 3 (mutta ei
suurempi).
Tehtävä 580
Käyrillä y = f(x) ja y = g(x) sanotaan olevan pisteessä x (vähintään) kertalukua n oleva kosketus, jos funktioiden arvot ja niiden derivaattojen arvot kertalukuun n saakka yhtyvät tässä pisteessä. Määritä seuraavista parvista se käyrä, jolla on mahdollisimman korkean kertaluvun kosketus käyrän y = ex kanssa kohdassa x = 0:| a) kaikki ympyrät, | |||
| b) paraabelit, joiden akselit ovat y-akselin suuntaiset, | |||
| c) paraabelit, joiden akselit ovat x-akselin suuntaiset, | |||
| d) kaikki paraabelit, | |||
| e) kaikki toisen asteen käyrät. |
Mikä on kosketuksen kertaluku?
Tehtävä 581
Käyrillä y = f(x) ja y = g(x) sanotaan olevan pisteessä x (vähintään) kertalukua n oleva kosketus, jos funktioiden arvot ja niiden derivaattojen arvot kertalukuun n saakka yhtyvät tässä pisteessä. Osoita, että niiden paraabelien polttopisteet, joilla on annetussa pisteessä toisen kertaluvun kosketus annetun käyrän kanssa, sijaitsevat ympyrällä, joka sivuaa käyrää annetussa pisteessä ja jonka säde on neljännes kyseiseen pisteeseen liittyvästä käyrän kaarevuussäteestä.13.3 Polynomiapproksimaatioista
Tehtävä 582
Eksponenttifunktiota ex approksimoidaan välillä [-1, 1] ensimmäisen asteen polynomilla ax + b. Määritä kertoimet a ja b siten, että saadaan paras tasainen approksimaatio, ts. approksimaatiovirheen maksimi on mahdollisimman pieni.13.4 Lagrangen interpolaatio
Tehtävä 583
Laske funktiolle f(x) = 1 + x - x2 tasaväliseen pisteistöön välillä [-1, 2] liittyvä a) ensimmäisen, b) toisen, c) kolmannen asteen interpolaatiopolynomi. Laske myös vastaavat virhetermit.Tehtävä 584
Funktiota f(x) = sin x interpoloidaan välillä [0, 1] tasavälisessä pisteistössä
astetta n olevalla polynomilla. Arvioi virhetermiä ja tutki, miten tämä käyttäytyy, kun n
kasvaa.
x interpoloidaan välillä [0, 1] tasavälisessä pisteistössä
astetta n olevalla polynomilla. Arvioi virhetermiä ja tutki, miten tämä käyttäytyy, kun n
kasvaa.
13.5 Numeerisesta integroinnista
Tehtävä 585
Tarkastele luvun ln 2 laskemista integraalin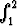 dx/x avulla: Laske
integraali numeerisesti a) Riemannin summana laskemalla funktion arvot osavälien
alkupisteissä, b) Riemannin summana laskemalla funktion arvot osavälien keskipisteissä,
c) puolisuunikassäännöllä, d) Simpsonin säännöllä. Jaa integroimisväli neljään, kahdeksaan
ja kuuteentoista osaväliin. Vertaa tuloksia.
dx/x avulla: Laske
integraali numeerisesti a) Riemannin summana laskemalla funktion arvot osavälien
alkupisteissä, b) Riemannin summana laskemalla funktion arvot osavälien keskipisteissä,
c) puolisuunikassäännöllä, d) Simpsonin säännöllä. Jaa integroimisväli neljään, kahdeksaan
ja kuuteentoista osaväliin. Vertaa tuloksia.
Tehtävä 586
Laske edellisen tehtävän numeerisen integroinnin virhetermit puolisuunnikassäännön ja Simpsonin säännön tapauksessa ja vertaa niitä todelliseen virheeseen.Tehtävä 587
Muodosta integraali, joka esittää ellipsin 4x2 + 9y2 = 36 kaarenpituutta. Laske tämä numeerisesti. (Integrointi alkeisfunktioiden avulla ei onnistu.)Tehtävä 588
Muodosta integraali, joka esittää ellipsin kehän pituutta eksentrisyyden funktiona, kun ison akselin puolikas on vakio a = 1. Piirrä kuvaaja, joka osoittaa, miten kehän pituus riippuu eksentrisyydestä. Mitkä ovat funktion tarkat arvot tarkasteluvälin päätepisteissä?Tehtävä 589
Muunna epäoleellinen integraali (jota ei voida integroida alkeisfunktioiden avulla)
 e-x2
dx
e-x2
dx
sijoituksella t = x/(1 + x) rajoitetun välin yli otetuksi integraaliksi ja laske se
numeerisesti jollakin tietokoneohjelmalla. Sijoituksen jälkeinen integraali on myös
epäoleellinen, mutta tästä aiheutuvat ongelmat voidaan väistää poistamalla
integroimisvälistä (todella) pieni osa singulariteetin ympäriltä. Vertaa tulosta tarkkaan
arvoon  /2.
/2.