2 Reaaliarvoiset funktiot
2.1 Jatkuvuus
Tehtävä 23
Tutki funktion
f(x, y) = 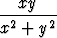
raja-arvoa, kun piste (x, y) lähestyy origoa pitkin seuraavia xy-tason käyriä: a) y = ax, b) y = ax2 , c) y2 = ax. Onko funktiolla raja-arvoa origossa?
Tehtävä 24
Tutki, onko seuraavilla kahden reaalimuuttujan reaaliarvoisilla funktioilla raja-arvoa origossa:
a) 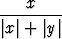 , b)
, b) 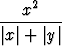 , c)
, c) 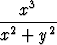 , d)
, d) 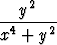 .
.
Tehtävä 25
Tarkastellaan funktiota f(x, y) = xy, missä x > 0, y > 0, (x, y)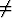 (0, 0).
Osoita, että funktiolla ei ole raja-arvoa origossa. Mitä arvoja funktio saa jokaisessa origon
ympäristössä? Piirrä funktion kuvaaja origon ympäristössä.
(0, 0).
Osoita, että funktiolla ei ole raja-arvoa origossa. Mitä arvoja funktio saa jokaisessa origon
ympäristössä? Piirrä funktion kuvaaja origon ympäristössä.
Tehtävä 26
Olkoon geometrisessa avaruudessa E3 määriteltynä reaaliarvoinen funktio
f(r) = 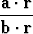 , b . r
, b . r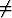 0,
0,
missä a ja b ovat lineaarisesti riippumattomia vakiovektoreita. Tutki, onko olemassa raja-arvoa
limr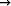 of(r).
of(r).
Tehtävä 27
Funktio f : 2
2 
 määritellään asettamalla f(0, 0) = a ja origon
ulkopuolella funktiolla on lauseke
määritellään asettamalla f(0, 0) = a ja origon
ulkopuolella funktiolla on lauseke
a) 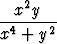 , b)
, b) 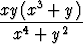 , c)
, c) 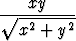 , d)
, d) 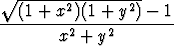 , e)
, e) 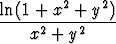 .
.
Voidaanko a valita siten, että f on jatkuva origossa?
Tehtävä 28
Tutki, voidaanko funktiot
a) 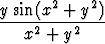 , b)
, b) 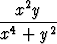 , c)
, c) 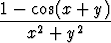 , d)
, d) 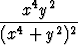
määritellä origossa siten, että niistä tulee jatkuvia. Piirrä funktioiden kuvaajat origon ympäristössä.
Tehtävä 29
Olkoon f : 2
2 
 ,
,
f(x, y) = 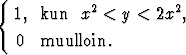
Osoita, että funktiolla on sama raja-arvo origossa lähestyttäessä mitä tahansa suoraa pitkin, mutta siitä huolimatta varsinainen raja-arvo ei ole olemassa. Missä pisteissä funktio ei ole jatkuva?
Tehtävä 30
Funktio f : n
n 
 olkoon jatkuva avoimessa joukossa G
olkoon jatkuva avoimessa joukossa G 
 n; olkoon
x0
n; olkoon
x0  G ja f(x0) > 0. Osoita, että on olemassa ympäristö U
G ja f(x0) > 0. Osoita, että on olemassa ympäristö U (x0) siten, että f(x) > 0, kun
x
(x0) siten, että f(x) > 0, kun
x  U
U (x0 ).
(x0 ).
Tehtävä 31
Funktio f : n
n 
 olkoon kaikkialla jatkuva; olkoot a ja b reaalilukuja,
a < b. Osoita, että joukko S = { x
olkoon kaikkialla jatkuva; olkoot a ja b reaalilukuja,
a < b. Osoita, että joukko S = { x 
 n | a < f(x) < b } on avoin. Määritä S tapauksessa
f :
n | a < f(x) < b } on avoin. Määritä S tapauksessa
f :  2
2 
 , f(x, y) = ex+2y, a = 1, b = 2.
, f(x, y) = ex+2y, a = 1, b = 2.
Tehtävä 32
Funktio f : n
n 
 olkoon kaikkialla jatkuva. Todista, että joukko
S = { x
olkoon kaikkialla jatkuva. Todista, että joukko
S = { x 
 n | f(x) = 0 } on suljettu. Määritä S tapauksessa f :
n | f(x) = 0 } on suljettu. Määritä S tapauksessa f :  3
3 
 ,
f(x, y, z) = x2 + y2 - z2.
,
f(x, y, z) = x2 + y2 - z2.
Tehtävä 33
Funktio f : n
n 
 olkoon jatkuva ja
olkoon jatkuva ja 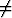 0 kompaktissa joukossa S
0 kompaktissa joukossa S 
 n.
Päättele, että on olemassa reaaliluku a > 0 siten, että |f(x)| > a kaikilla x
n.
Päättele, että on olemassa reaaliluku a > 0 siten, että |f(x)| > a kaikilla x  S. Onko
tulos voimassa, jos S ei ole kompakti? Esitä esimerkkejä.
S. Onko
tulos voimassa, jos S ei ole kompakti? Esitä esimerkkejä.
Tehtävä 34
Funktio f : n
n 
 olkoon kaikkialla jatkuva ja sillä olkoon ominaisuudet
olkoon kaikkialla jatkuva ja sillä olkoon ominaisuudet
lim||x||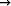
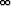 f(x) = 0,
f(x) = 0, 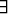 x1, x2
x1, x2 
 n siten, että f(x1)f(x2) < 0.
n siten, että f(x1)f(x2) < 0.
Päättele, että funktion arvojoukolla { f(x) | x 
 n } on maksimi ja minimi. Päteekö
tulos, jos luovutaan funktion jatkuvuudesta tai jommastakummasta lisäominaisuudesta?
Esitä esimerkkejä.
n } on maksimi ja minimi. Päteekö
tulos, jos luovutaan funktion jatkuvuudesta tai jommastakummasta lisäominaisuudesta?
Esitä esimerkkejä.
Tehtävä 35
Funktio f : 2
2 
 olkoon kaikkialla jatkuva ja sillä olkoon ominaisuus
olkoon kaikkialla jatkuva ja sillä olkoon ominaisuus
f(x, y) < 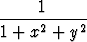
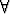 x, y
x, y 
 .
.
Osoita, että on olemassa reaaliluku a < 1 siten, että f(x, y) < a kaikilla (x, y) 
 2.
2.
2.2 Osittaisderivaatat
Tehtävä 36
Muodosta seuraavien funktioiden osittaisderivaatat kaikkien esiintyvien muuttujien suhteen:| a) xy3 + x sin(xy), | b) ln sin(x - 2y), | c) 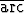 sin sin 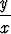 , , | d) logyx, | ||||||||||||
| e) (xy)z, | f) zxy, | g) xyx , | h) xyz . |
Tehtävä 37
Laske kunkin funktion tapauksessa annettu osittaiderivaattalauseke ja saata se mahdollisimman yksinkertaiseen muotoon:a) f(x, y) = ln(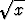 + + 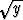 ), xfx + yfy, ), xfx + yfy, | |||
| b) f(x, y, z) = ln(x3 + y3 + z3 - 3xyz), fx + fy + fz, | |||
c) f(x, y, z) =  x/z, xfx + yfy + zfz. x/z, xfx + yfy + zfz. |
Tehtävä 38
Tutki, ovatko funktiot a) f(x, y) =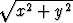 , b) (x + y)|x + y| derivoituvia
origossa? Entä jatkuvasti derivoituvia?
, b) (x + y)|x + y| derivoituvia
origossa? Entä jatkuvasti derivoituvia?
Tehtävä 39
Missä suoran y = x pisteissä funktiolla f(x, y) = |x2 - y2| on osittaisderivaatat fx ja fy ?Tehtävä 40
Määritä funktion
f(x, y) = 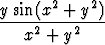 , kun (x, y)
, kun (x, y)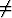 (0, 0), f(0, 0) = 0
(0, 0), f(0, 0) = 0
osittaisderivaatat kaikkialla ja osoita, että ne ovat jatkuvia.
Tehtävä 41
Olkoon f(x, y) = x3y2 + x4 sin y + cos(xy). Laske osittaisderivaatat fxxy, fxyx, fyxx ja totea, että nämä ovat yhtä suuria.Tehtävä 42
Laske funktion f(x, y) = xy ensimmäisen ja toisen kertaluvun osittaisderivaatat, kun x > 0, y
 . Ovatko toisen kertaluvun sekaderivaatat yhtä suuria?
. Ovatko toisen kertaluvun sekaderivaatat yhtä suuria?
Tehtävä 43
Laske funktion
f(x, y) = xy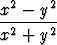 , kun (x, y)
, kun (x, y)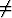 (0, 0), f(0, 0) = 0
(0, 0), f(0, 0) = 0
ensimmäisen kertaluvun osittaisderivaatat origossa ja muualla. Laske toisen kertaluvun sekaderivaatat fxy(0, 0) ja fyx(0, 0); totea, että nämä ovat eri suuret. Piirrä funktion kuvaaja.
Tehtävä 44
Osoita, että funktiot a) ln(x2 + y2), b)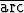 tan
tan 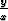 , c) eax cos(ay) (a vakio) ovat
Laplacen differentiaaliyhtälön
, c) eax cos(ay) (a vakio) ovat
Laplacen differentiaaliyhtälön
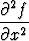 +
+ 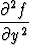 = 0
= 0
ratkaisuja eli ns. harmonisisia funktioita.
Tehtävä 45
Osoita, että funktio f(x, t) = u(x + at) + v(x - at), missä u ja v ovat kahdesti derivoituvia funktioita

 ja a vakio, toteuttaa osittaisdifferentiaaliyhtälön
ftt = a2 fxx.
ja a vakio, toteuttaa osittaisdifferentiaaliyhtälön
ftt = a2 fxx.
Tehtävä 46
Olkoot f ja g kahdesti jatkuvasti derivoituvia funktioita

 . Määritä
vakiot a ja k siten, että funktio u(x, y) = xf(x + ay) + yg(x + ay) toteuttaa
osittaisdifferentiaaliyhtälön
. Määritä
vakiot a ja k siten, että funktio u(x, y) = xf(x + ay) + yg(x + ay) toteuttaa
osittaisdifferentiaaliyhtälön
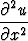 +
+ 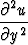 = k
= k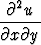 .
.
Tehtävä 47
Osoita, että funktio u(x, y) = xf(x + y) + yg(x + y) toteuttaa osittaisdifferentiaaliyhtälön
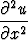 +
+ 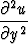 = 2
= 2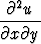
olivatpa f ja g mitä tahansa kahdesti jatkuvasti derivoituvia funktioita 

 .
.
Tehtävä 48
Olkoot u ja v derivoituvia funktioita

 . Osoita, että funktio f :
. Osoita, että funktio f :  2
2 
 ,
f(x, y) = u(x) + v(y), toteuttaa differentiaaliyhtälön
,
f(x, y) = u(x) + v(y), toteuttaa differentiaaliyhtälön
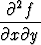 = 0.
= 0.
Osoita kääntäen, että jokaisella tämän differentiaaliyhtälön ratkaisulla on em. muoto.
2.3 Differentiaalikehitelmä
Tehtävä 49
Laske funktion lisäys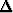 f, differentiaali df ja korjaustermi, kun f(x, y) = x2y,
x = 1, y = 3,
f, differentiaali df ja korjaustermi, kun f(x, y) = x2y,
x = 1, y = 3, 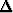 x = 0.2 ja
x = 0.2 ja 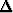 y = -0.1.
y = -0.1.
Tehtävä 50
Muodosta seuraavien funktioiden (kokonais)differentiaalit:
a) 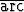 tan yx, b)
tan yx, b) 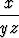 , c) xy ln z, d) ln tan
, c) xy ln z, d) ln tan 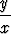 .
.
Tehtävä 51
Arvioi differentiaalin avulla lausekkeen
z = ex sin y 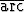 tan x
tan x
arvoa, kun x = 1 ± 0.001 ja y = 30 ± 0.02o.
Tehtävä 52
Osoita suoraan differentioituvuuden määritelmän perusteella, että funktio f(x, y) = x cos y on differentioituva koko tasossa 2.
2.
Tehtävä 53
Olkoon f :

 jatkuvasti derivoituva funktio. Määritellään funktio
g :
jatkuvasti derivoituva funktio. Määritellään funktio
g :  2
2 
 asettamalla
asettamalla
g(x, y) = 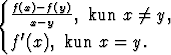
Osoita, että g on differentioituva pisteessä (a, a), jos f''(a) on olemassa.
Tehtävä 54
Missä tason 2 pisteissä funktio f(x, y) = max{|x|, |y|} on differentioituva?
2 pisteissä funktio f(x, y) = max{|x|, |y|} on differentioituva?
Tehtävä 55
Määritä funktion f : 2
2 
 ,
,
f(x, y) = (x2 + y2) sin 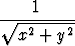 , kun (x, y)
, kun (x, y)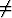 (0, 0), f(0, 0) = 0
(0, 0), f(0, 0) = 0
osittaisderivaatat origossa. Osoita, että funktio on differentioituva. Osoita, että osittaisderivaatat eivät ole jatkuvia origossa.
Tehtävä 56
Olkoon
f(x, y) = 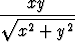 , kun (x, y)
, kun (x, y)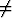 (0, 0), f(0, 0) = 0.
(0, 0), f(0, 0) = 0.
Määritä funktion osittaisderivaatat origossa ja osoita, että funktio ei ole differentioituva origossa. Piirrä funktion kuvaaja.
Tehtävä 57
Olkoon reaaliarvoinen funktio f määritelty avoimessa joukossa G
 n ja
differentioituva pisteessä x0
n ja
differentioituva pisteessä x0  G. Todista, että tällöin f toteuttaa Lipschitzin ehdon
pisteessä x0 : On olemassa vakio M > 0 ja ympäristö U
G. Todista, että tällöin f toteuttaa Lipschitzin ehdon
pisteessä x0 : On olemassa vakio M > 0 ja ympäristö U (x0) siten, että
(x0) siten, että
|f(x) - f(x0)| < M||x - x0|| 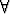 x
x  U
U (x0).
(x0).
Tehtävä 58
Laske funktion f : 2
2 
 , f(x, y) = x4 + 2y2 + 4xy differentiaali
pisteessä (-3, 2). Mikä on tämän yhteys pinnan z = f(x, y) tangenttitasoon?
, f(x, y) = x4 + 2y2 + 4xy differentiaali
pisteessä (-3, 2). Mikä on tämän yhteys pinnan z = f(x, y) tangenttitasoon?
Tehtävä 59
Laske seuraavien funktioiden suunnatut derivaatat annettuihin suuntiin annetuissa pisteissä:| a) f(x, y) = ex+y, i + j, (0, 0), | |||
b) f(x, y) = sin( x) cos( x) cos( y2), i - 2j, (1, 2), y2), i - 2j, (1, 2), | |||
| c) f(x, y, z) = xy2z3, 6i - 2j + 3k, (-3, 2, 1), | |||
| d) f(x, y, z) = xy2 + yz3, i + j - 2k, (3, -1, 4). |
Tehtävä 60
Laske funktion f(x, y, z) = xy + cos x + y2z ensimmäisen kertaluvun osittaisderivaatat ja gradientti pisteessä ( /2, 1, -
/2, 1, - /2). Mitä gradientti ilmaisee
funktiosta f ? Entä pinnasta f(x, y, z) = 0 ?
/2). Mitä gradientti ilmaisee
funktiosta f ? Entä pinnasta f(x, y, z) = 0 ?
Tehtävä 61
Mihin suuntaan funktio f(x, y, z) = x3 - 2xy2z + 5yz4 kasvaa nopeimmin pisteessä (2, -2, 1)? Mikä on funktion derivaatta tähän suuntaan? Piirrä funktion kuvaaja, kun se rajoitetaan tämän suuntaiselle ko. pisteen kautta kulkevalle suoralle.Tehtävä 62
Olkoon f : 3
3 
 , f(x, y, z) = xy2 + yz3. Tutki, mihin suuntaan
pisteestä (3, -1, 4) on edettävä, jotta a) funktio kasvaisi mahdollisimman nopeasti,
b) funktio ei kasvaisi lainkaan. Mikä on funktion derivaatta nopeimman kasvun
suuntaan?
, f(x, y, z) = xy2 + yz3. Tutki, mihin suuntaan
pisteestä (3, -1, 4) on edettävä, jotta a) funktio kasvaisi mahdollisimman nopeasti,
b) funktio ei kasvaisi lainkaan. Mikä on funktion derivaatta nopeimman kasvun
suuntaan?
Tehtävä 63
Tutki, mihin suuntaan v funktio f(x, y, z) = xy2 + yz3 kasvaa nopeimmin pisteessä P (3, -1, 2). Muodosta yhden muuttujan funktio, joka kuvaa funktion f
käyttäytymistä pisteen P kautta kulkevalla vektorin v suuntaisella suoralla; valitse
argumentiksi etäisyys pisteestä P (positiivisena vektorin v suuntaan, negatiivisena
vastakkaiseen suuntaan).
(3, -1, 2). Muodosta yhden muuttujan funktio, joka kuvaa funktion f
käyttäytymistä pisteen P kautta kulkevalla vektorin v suuntaisella suoralla; valitse
argumentiksi etäisyys pisteestä P (positiivisena vektorin v suuntaan, negatiivisena
vastakkaiseen suuntaan).
Tehtävä 64
Etsi pisteet, joissa funktion f(x, y, z) = xy + cos x + y2z gradientti on yz-tason suuntainen.Tehtävä 65
Tutki gradienttia käyttäen, missä pisteissä käyrän x3 + y3 - 3xy = 0 tangentti on a) pystysuora, b) vaakasuora, c) kaltevuudeltaan 45o.Tehtävä 66
Mihin suuntiin funktion f(x, y) = 2x - y2 suunnattu derivaatta origossa on = 0?Tehtävä 67
Mihin suuntiin funktion f : 2
2 
 ,
,
f(x, y) = 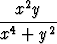 , kun (x, y)
, kun (x, y)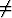 (0, 0), f(0, 0) = 0,
(0, 0), f(0, 0) = 0,
origossa muodostettu suunnattu derivaatta on olemassa? Onko f differentioituva origossa?
Tehtävä 68
Olkoon f : n
n 
 differentioituva pisteessä x0
differentioituva pisteessä x0 
 n ja grad f(x0)
n ja grad f(x0)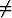 O.
Osoita, että on olemassa täsmälleen yksi yksikkövektori w
O.
Osoita, että on olemassa täsmälleen yksi yksikkövektori w 
 n siten, että suunnattu
derivaatta suuntaan w pisteessä x0 on = || grad f(x0)||.
n siten, että suunnattu
derivaatta suuntaan w pisteessä x0 on = || grad f(x0)||.
Tehtävä 69
Graafisen esityksen perusteella on käyrän y = f(x) ensimmäiselle ja toiselle derivaatalle saatu tarkastelukohdan ympäristössä arviot2.995 < f'(x) < 3.005, 1.99 < f''(x) < 2.01.
Määritä differentiaalia käyttäen likimääräiset virherajat käyrän kaarevuussäteelle kyseisessä kohdassa.
Tehtävä 70
Helsingin ja Tokion maantieteelliset koordinaatit asteen tarkkuudella ovat seuraavat:| Helsinki: | 60o | N , | 25o | E ; | |||||||
| Tokio: | 36o | N , | 140o | E . |
Maapallon säde on 6370 km kymmenen kilometrin tarkkuudella. Arvioi kokonaisdifferentiaalia käyttäen, millä tarkkuudella kaupunkien lyhin etäisyys maapallon pintaa pitkin mitattuna voidaan näistä tiedoista laskea, kun oletetaan maa täysin pallonmuotoiseksi.
Tehtävä 71
Pisteen B etäisyys pisteestä A määritettiin kolmannen pisteen C avulla. Mittaustulokset olivat
|BC| = 265 ± 0.5 m, 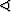 ACB = 45 ± 0.1o,
ACB = 45 ± 0.1o, 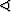 ABC = 105 ± 0.1o.
ABC = 105 ± 0.1o.
Laske pisteiden A ja B välinen etäisyys ja sille suhteellinen virheraja.
Tehtävä 72
Pystysuoran lipputangon varjo vaakasuoralla kentällä havaitaan kahtena ajankohtana. Tänä aikana varjo on kiertynyt kulman 21o30', auringon korkeuskulma vähentynyt arvosta 35o30' arvoon 29o0' ja varjon pää piirtänyt kaaren, jonka jänteen pituus on 784 cm. Mikä on tangon korkeus ja millä tarkkuudella se em. arvoista saadaan, kun kulmamittausten tarkkuus on 15' ja pituusmittauksen 2 cm?Tehtävä 73
Miten tarkkoja lukujen e ja likiarvoja on käytettävä, jotta luvun a) e
likiarvoja on käytettävä, jotta luvun a) e , b) e
, b) e virhe olisi < 0.005?
virhe olisi < 0.005?
Tehtävä 74
Karttapaperi kutistuu x-akselin suunnassa 1 % ja y-akselin suunnassa 0.6 %. Arvioi kokonaisdifferentiaalia käyttäen, kuinka monta prosenttia on korjattava sellaista etäisyyttä, joka kutistuneella kartalla muodostaa 30 asteen kulman x-akselin kanssa? Montako astetta kulmaa on korjattava?2.4 Väliarvolause
Tehtävä 75
Olkoon f(x, y) = x2 + 2y2 - xy. Etsi väliarvolausessa mainittu piste (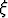 ,
, 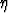 ),
jolle pätee
),
jolle pätee
f(x, y) - f(0, 0) = fx(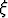 ,
, 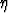 )x + fy(
)x + fy(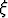 ,
, 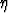 )y.
)y.
Tehtävä 76
Funktiot f : n
n 
 ja g :
ja g :  n
n 
 olkoot differentioituvia alueessa G
olkoot differentioituvia alueessa G 
 n.
Osoita, että jos kaikilla x
n.
Osoita, että jos kaikilla x  G pätee
G pätee
fxk(x) = gxk(x), k = 1, . . . , n,
niin on olemassa vakio C siten, että f(x) = g(x) + C alueessa G.
2.5 Ketjusääntö
Tehtävä 77
Laske ketjusääntöä käyttäen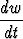 , kun
, kun
| a) w = xy + yz + zx, x = et, y = 2t2, z = e-t, | |||
b) w = 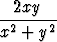 , x = 2t, y = t2, , x = 2t, y = t2, | |||
| c) w = ln(x2 + 3xy2 + 4y4), x = 2t2, y = 3t. |
Tehtävä 78
Laske ketjusääntöä käyttäen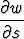 ja
ja 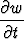 , kun
, kun
| a) w = x ln(x2 + y2), x = s + t, y = s - t, | |||
| b) w = ex+2y sin(2x - y), x = s2 + 2t2, y = 2s2 - t2. |
Tehtävä 79
Kappale kulkee pinnalla F (x, y, z) = 0 siten, että sen x- ja y-koordinaattien aikariippuvuus tunnetaan: x = x(t), y = y(t). Lausu kappaleen nopeusvektori funktioiden F , x ja y derivaattojen avulla. Sovella tulosta tapaukseen, missä pinta on yksikkösäteinen pallo ja x- ja y-koordinaatit kasvavat aikaan verrannollisesti: x(t) = y(t) = t. Liike alkaa hetkellä t = 0. Hahmottele nopeusvektorin itseisarvon kuvaaja.Tehtävä 80
Olkoon u(x, y) = sin x + f(sin y - sin x), missä f :

 on differentioituva
funktio. Osoita, että lauseke uy cos x + ux cos y on riippumaton funktiosta f.
on differentioituva
funktio. Osoita, että lauseke uy cos x + ux cos y on riippumaton funktiosta f.
Tehtävä 81
Olkoot f ja g kaksi kahdesti derivoituvaa funktiota

 ja olkoon
h(x, y) = f(xg(y)). Laske funktion h toisen kertaluvun osittaisderivaatat.
ja olkoon
h(x, y) = f(xg(y)). Laske funktion h toisen kertaluvun osittaisderivaatat.
Tehtävä 82
Osoita, että funktio z =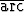 tan
tan 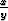 , missä x = u + v, y = u - v, toteuttaa
osittaisdifferentiaaliyhtälön
, missä x = u + v, y = u - v, toteuttaa
osittaisdifferentiaaliyhtälön
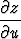 +
+ 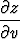 =
= 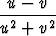 .
.
Tehtävä 83
Kahdesti jatkuvasti derivoituva funktio f(x, t) toteuttaa aaltoyhtälön
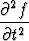 = c2
= c2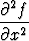 .
.
Merkitään u = x + ct, v = x - ct, f(x, t) = F (u, v). Etsi osittaisdifferentiaaliyhtälö funktiolle F .
Tehtävä 84
Olkoon u(x, y) kahdesti jatkuvasti derivoituva reaaliarvoinen funktio, joka tasossa 2 toteuttaa osittaisdifferentiaaliyhtälön
2 toteuttaa osittaisdifferentiaaliyhtälön
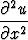 =
= 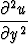 .
.
Merkitään x = s + t, y = s - t ja u(x, y) = u(s + t, s - t) = U(s, t). Muunna osittaisdifferentiaaliyhtälö funktiota U koskevaksi ja ratkaise se. Millainen ratkaisu tästä saadaan alkuperäisen yhtälön tuntemattomalle funktiolle u ?
Tehtävä 85
Olkoon f koko xy-tasossa määritelty funktio ja olkoon tämän esitys napakoordinaattien avulla f(x, y) = f(r cos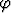 , r sin
, r sin 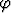 ) = F (r,
) = F (r, 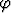 ). a) Lausu funktion f
osittaisderivaatat funktion F osittaisderivaattojen ja muuttujien r,
). a) Lausu funktion f
osittaisderivaatat funktion F osittaisderivaattojen ja muuttujien r, 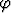 avulla. b) Lausu
funktion F osittaisderivaatat funktion f osittaisderivaattojen ja muuttujien x, y avulla.
avulla. b) Lausu
funktion F osittaisderivaatat funktion f osittaisderivaattojen ja muuttujien x, y avulla.
Tehtävä 86
Lausutaan funktio f(x, y) napakoordinaattien avulla:
f(x, y) = f(r cos 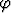 , r sin
, r sin 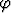 ) = F (r,
) = F (r, 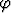 ).
).
Esitä lauseke
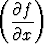 2 +
2 + 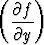 2
2
napakoordinaattien ja funktion F osittaisderivaattojen avulla.
Tehtävä 87
Suure S voidaan esittää sekä suorakulmaisten että napakoordinaattien avulla: S = f(x, y) = F (r,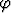 ). Se toteuttaa suorakulmaisten koordinaattien suhteen
osittaisdifferentiaaliyhtälön
). Se toteuttaa suorakulmaisten koordinaattien suhteen
osittaisdifferentiaaliyhtälön
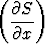 2 +
2 + 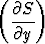 2 = 1.
2 = 1.
Millaisen napakoordinaattien suhteen muodostetun osittaisdifferentiaaliyhtälön se toteuttaa?
Tehtävä 88
Funktio u(x, y) on tason 2 pisteissä määritelty skalaarikenttä;
napakoordinaattien avulla lausuttuna tämä on U(r,
2 pisteissä määritelty skalaarikenttä;
napakoordinaattien avulla lausuttuna tämä on U(r, 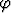 ). Lausu napakoordinaateissa
). Lausu napakoordinaateissa
a) x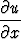 - y
- y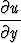 , b) x
, b) x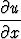 + y
+ y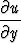 , c)
, c) 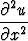 +
+ 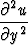 .
.
Tehtävä 89
Muunna osittaisdifferentiaaliyhtälö
x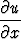 + y
+ y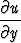 = x2 + y2
= x2 + y2
napakoordinaatteihin. Merkitse tällöin u(x, y) = U(r, 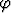 ). Millaisia ratkaisuja yhtälöllä
on? Oletetaan lisäksi, että ratkaisufunktio saa xy-tason yksikköympyrällä arvot
u(x, y) = x. Onko u tällöin jatkuva origossa?
). Millaisia ratkaisuja yhtälöllä
on? Oletetaan lisäksi, että ratkaisufunktio saa xy-tason yksikköympyrällä arvot
u(x, y) = x. Onko u tällöin jatkuva origossa?
Tehtävä 90
Funktio f(x, y) toteuttaa alueessa { (x, y) | x > 0, y > 0 } osittaisdifferentiaaliyhtälön
x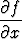 = y
= y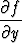 .
.
Lisäksi pätee f(x, x) = x, kun x > 0. Muunna yhtälö sijoituksella u = xy, v = y/x funktiota F (u, v) = f(x, y) koskevaksi ja ratkaise f(x, y). Onko funktiolla f raja-arvoa origossa?
Tehtävä 91
Olkoon skalaarikenttä u muotoa u(x, y, z) = f(r), missä r =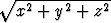 ja
f on derivoituva. Kenttä toteuttakoon osittaisdifferentiaaliyhtälön
ja
f on derivoituva. Kenttä toteuttakoon osittaisdifferentiaaliyhtälön
x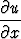 + y
+ y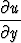 + z
+ z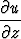 = u.
= u.
Muunna tämä funktiota f koskevaksi differentiaaliyhtälöksi, jossa muuttujana on r. Ratkaise yhtälö. Minkälainen lauseke saadaan kentälle u?
Tehtävä 92
Olkoon f geometrisessa avaruudessa E3 määritelty funktio: f(r) = f(x, y, z) = g(r), missä g :

 on derivoituva yhden muuttujan funktio ja
paikkavektorin r = x i + y j + z k pituus on r =
on derivoituva yhden muuttujan funktio ja
paikkavektorin r = x i + y j + z k pituus on r = 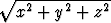 . Funktio f riippuu siis vain
origosta mitatusta etäisyydestä. Osoita:
. Funktio f riippuu siis vain
origosta mitatusta etäisyydestä. Osoita:
grad f = g'(r)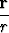 .
.
Tehtävä 93
Funktio f(x, y) toteuttaa osittaisdifferentiaaliyhtälön
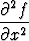 - 4x
- 4x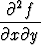 + 4x2
+ 4x2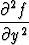 - 2
- 2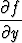 = 0.
= 0.
Olkoot u = x2 + y ja v = x uudet muuttujat; siis x = v, y = u - v2. Merkitään f(x, y) = f(v, u - v2) = F (u, v). Millaisen osittaisdifferentiaaliyhtälön toteuttaa funktio F ?