3 Taylorin polynomi; funktion ääriarvot
3.1 Taylorin polynomi
Tehtävä 94
Kehitä funktio f(x, y) = x2y3 Taylorin polynomiksi kehityskeskuksena piste (-1, 2) a) laskemalla osittaisderivaatat, b) kirjoittamalla muuttujat muotoon x = -1 + (x + 1), y = 2 + (y - 2).Tehtävä 95
Laske Taylorin polynomit seuraavissa tapauksissa:| a) f(x, y) = 2x4 - 5y3 + 2xy2, keskus = (0, 0), aste = 3; | |||
| b) f(x, y) = y2 ln x, keskus = (1, 0), aste = 4; | |||
c) f(x, y) = 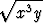 , keskus = (1, 3), aste = 4. , keskus = (1, 3), aste = 4. |
Tehtävä 96
Laske termin (x + )2(y -
)2(y -  )2 kerroin funktion f(x, y) = sin(x cos y)
tekijöiden x +
)2 kerroin funktion f(x, y) = sin(x cos y)
tekijöiden x +  ja y -
ja y -  mukaan etenevässä Taylorin kehitelmässä.
mukaan etenevässä Taylorin kehitelmässä.
Tehtävä 97
Muodosta funktion ex+2y toisen asteen Taylorin polynomi pisteessä (0, 0) sekä Taylorin lauseen mukainen lauseke funktion ja polynomin erotukselle. Etsi erotuksen itseisarvolle yläraja neliössä -1 < x < 1, -1 < y < 1.Tehtävä 98
Etsi funktion
f(x, y, z) = 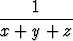
kolmannen asteen Taylorin polynomi pisteessä (1, 0, 0) laskemalla kertoimet osittaisderivaattojen avulla.
Tehtävä 99
Etsi funktion
f(x, y, z) = 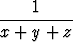
kolmannen asteen Taylorin polynomi pisteessä (1, 0, 0) käyttämällä hyväksi yhden muuttujan funktion 1/(1 + t) Maclaurinin polynomia.
Tehtävä 100
Muodosta funktiolle
f(x, y, z) = 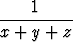 =
= 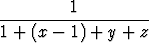
neljännen asteen Taylorin polynomi pisteessä (1, 0, 0) käyttämällä hyväksi funktion 1/(1 + t) Taylorin polynomia. Laske tämän avulla fxyzz(1, 0, 0).
Tehtävä 101
Muodosta funktion f(x, y) = sin(xy) kuudennen asteen Taylorin polynomi pisteessä (0, 0) käyttämällä funktion sin t Taylorin polynomia. Laske tämän avulla kaikki funktion kuudennen kertaluvun osittaisderivaatat origossa.Tehtävä 102
Muodosta funktiollef(x, y) = exy sin y
kolmannen asteen Taylorin polynomi kehityskeskuksena origo käyttämällä yhden muuttujan funktioiden et ja sin t Maclaurinin polynomeja.
Tehtävä 103
Laske funktion f(x, y) = ln(1 + x2 + y2) osittaisderivaatta fxxxxxxyy(0, 0) muodostamalla funktiolle riittävän korkeata astetta oleva Taylorin polynomi. Muodosta tätä varten ensin funktion ln(1 + t) Taylorin polynomi.Tehtävä 104
Yhtälö x2 + 2y2 + 3z2 = 6 määrittelee eräässä pisteen (1, 1, 1) ympäristössä funktion z = f(x, y). Muodosta tämän funktion toisen asteen Taylorin polynomi pisteessä (1, 1).Tehtävä 105
Laske funktion f(x, y, z) origokeskisen Taylorin polynomin neljännen asteen termien kertoimet. Vrt. näitä ns. multinomikertoimiin.Tehtävä 106
Tarkastellaan funktiota f : 2
2 
 pisteen (x0, y0) ympäristössä.
Merkitään h = (x - x0, y - y0) = (hx, hy). Osoita, että jos tässä ympäristössä on
voimassa
pisteen (x0, y0) ympäristössä.
Merkitään h = (x - x0, y - y0) = (hx, hy). Osoita, että jos tässä ympäristössä on
voimassa
| f(x, y) = A0 + A1(hx, hy) + . . . + An(hx, hy) + u(x, y)||h||n+1, | |||
| f(x, y) = B0 + B1(hx, hy) + . . . + Bn(hx, hy) + v(x, y)||h||n+1, |
missä Aj ja Bj ovat astetta j olevia homogeenisia kahden muuttujan polynomeja ja funktiot u ja v ovat rajoitettuja, niin kehitelmät ovat identtiset.
3.2 Funktion suhteelliset ääriarvot
Tehtävä 107
Luokittele seuraavat neliömuodot:a) 2x2 - 7xy - 15y2, b) 6xy - 9x2 - y2, c) 4xy - 2x2 - 3y2.
Missä neliömuodot ovat = 0?
Tehtävä 108
Luokittele seuraavat neliömuodot:a) 2x2 + 2y2 + z2 - 4xy + 6yz, b) x2 + 2y2 + 3z2 - 2yz + 2zx.
Tehtävä 109
Etsi funktion f(x, y) = 2xy - x2 - y4 lokaalit ääriarvot. Piirrä funktion kuvaaja.Tehtävä 110
Etsi seuraaville funktioille f ne pisteet, joissa grad f = O, ja tutki lokaalin ääriarvon esiintymistä:| a) y4 + x2 - 2xy, | b) x3 + xy + y2 - 3x - 9y, | c) x4 + y4 + 4xy - 2y2, | |||||||||
| d) (x + 2y - 2)(x - 2)(y - 1), | e) 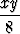 + + 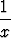 - - 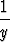 , , | f) (x + y)e-x2-y2 . |
Tehtävä 111
Määritä funktionf(x, y) = (x2 - y2)e(-x2-y2)/2
lokaalit ääriarvokohdat, näiden laatu sekä ääriarvot.
Tehtävä 112
Millä vakion a arvoilla funktiollaf(x, y) = ex2 - 2 cos y + axy
on suhteellinen minimikohta origossa?
Tehtävä 113
Tutki funktion f(x, y) = x3 + 3axy2 - 3x2 - 3y2 + 4 suhteellisia ääriarvokohtia vakion a eri arvoilla. Määritä ääriarvojen laatu neliömuotojen teoriaa käyttäen. Onnistutaanko tällöin kaikissa tapauksissa?Tehtävä 114
Tutki, onko piste (2, 0) funktion
f(x, y) = x3 +  xy2 - 3x2 - 3y2 + 4
xy2 - 3x2 - 3y2 + 4
ääriarvopiste. Millainen tulos saadaan neliömuotojen teorian avulla? Piirrä pinnasta korkeuskäyräkuva.
Tehtävä 115
Tutki neliömuotoja käyttäen, onko origo suhteellinen ääriarvo funktiollef(x, y, z) = ex2 + ey2 + ez2 - xy.
Jos on, onko kyseessä maksimi vai minimi?
Tehtävä 116
Tutki, onko origo suhteellinen ääriarvokohta funktiolle
f(x, y) =  (x3 + xy2)k.
(x3 + xy2)k.
Tehtävä 117
Osoita, että funktiolla f(x, y) = (x2 - y)(2x2 - y) ei ole ääriarvoa origossa, vaikka sen rajoittumalla jokaiselle origon kautta kulkevalle suoralle on suhteellinen minimi.3.3 Absoluuttiset ääriarvot
Tehtävä 118
Etsi seuraavien funktioiden maksimi ja minimi annetussa joukossa:| a) xy + x - y, { (x, y) | x2 + y2 < 1, x + y + 1 > 0, x - y - 1 < 0 }; | |||
| b) x2 - 2y2 - xy - x, { (x, y) | x > -1, y > -1, x + y < 1 }; | |||
| c) 3 + x - x2 - y2, { (x, y) | 2x2 + y2 < 1 }; | |||
| d) y2 - 2x2, { (x, y) | x2 - y < 1, x + y < 1 }; | |||
| e) xy(a - x - y), { (x, y) | |x| < a, |y| < a }; | |||
| f) x3 + y3, { (x, y) | 0 < xy < 1, x2 + y2 < 4 }; | |||
g) sin x + sin y - sin(x + y), { (x, y) | 0 < x <  , 0 < y < , 0 < y <  }; }; | |||
| h) (x + y)ey, { (x, y) | |x| < 1, |y| < 1 }; | |||
| i) x sin z + y cos z, { (x, y, z) | x2 + y2 + z2 < 1 }. |
Tehtävä 119
Määritä funktionf(x, y) = xe-x2-y2
suuurin ja pienin arvo ympyrässä x2 + y2 < R2.
Tehtävä 120
Määritä funktion f(x, y) = x2 + y2 + 2axy suurin ja pienin arvo ympyrässä { (x, y) | x2 + y2 < 1 } kaikilla vakion a arvoilla.Tehtävä 121
Paraboloidisegmentistä x2 + 4y2 < z < 1 sahataan suorakulmainen särmiö, jonka sivutahkot ovat koordinaattitasojen suuntaiset. Määritä tämän suurin mahdollinen tilavuus. Mitkä ovat tällöin särmiön mitat?Tehtävä 122
Suorakulmaisen särmiön sivutahkot ovat koordinaattitasojen suuntaiset ja se sijaitsee ellipsoidin x2/a2 + y2/b2 + z2/c2 = 1 sisässä. Miten suuri voi särmiön tilavuus olla? Mitkä ovat tällöin sen särmien pituudet?Tehtävä 123
Määritä funktion
f(x, y) = 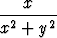
suurin ja pienin arvo joukossa
a) { (x, y) | 0 < x2 + y2 < 1 }, b) { (x, y) | x2 + y2 > 1 }, c)  2 \ {(0, 0)},
2 \ {(0, 0)},
mikäli nämä ovat olemassa.
Tehtävä 124
Määritä funktion
a) f(x, y) = (x + y)e-x2-y2
, b) f(x, y) = 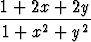
suurin ja pienin arvo tasossa  2, mikäli nämä ovat olemassa.
2, mikäli nämä ovat olemassa.
Tehtävä 125
Osoita, että reaalilukujoukon{ xye-x2y | x > 0, 0 < y < 1 }
maksimi on olemassa ja määritä se.