4 Vektoriarvoiset funktiot
4.1 Differentioituvuus
Tehtävä 127
Olkoot f : n
n 
 p ja g :
p ja g :  n
n 
 p differentioituvia funktioita. Todista
differentiaalikehitelmää käyttäen, että myös summa f + g on differentioituva
ja
p differentioituvia funktioita. Todista
differentiaalikehitelmää käyttäen, että myös summa f + g on differentioituva
ja
d(f + g) = df + dg.
Tehtävä 128
Laske seuraavien vektorimuuttujan vektoriarvoisten funktioiden Jacobi’n matriisit:
a) f(x, y, z) = (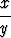 , 2y + 1, xz2), b) f(x, y, z) = (xe-yz,
, 2y + 1, xz2), b) f(x, y, z) = (xe-yz, 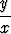 +
+ 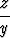 ,
, 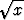 z2).
z2).
Tehtävä 129
Etsi vektorimuuttujan vektoriarvoisen funktionf(x, y, z) = (x2 + yz, 2zex, x ln y)
Jacobi’n matriisi. Laske funktion differentiaali pisteessä (0, 1, -2), kun 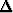 x =
x = 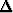 y =
y = 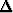 z = 0.1.
z = 0.1.
Tehtävä 130
Linearisoi funktio f : 2
2 
 2, f(x, y) = (x3y5 - 1, x7 + y7 - 5), ts. laske sen
differentiaali.
2, f(x, y) = (x3y5 - 1, x7 + y7 - 5), ts. laske sen
differentiaali.
Tehtävä 131
Funktiot f : n
n 
 n ja g :
n ja g :  n
n 
 määritellään seuraavasti:
määritellään seuraavasti:
f(x) = 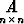 x +
x + 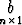 , g(x) = xT
, g(x) = xT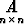 x.
x.
Määritä funktioiden derivaatat, so. Jacobi’n matriisit.
Tehtävä 132
Käänteissäteinen muunnos (eli inversiokuvaus) on kuvaus 2 \ {(0, 0)}
2 \ {(0, 0)} 
 2,
missä pisteen P kuvaksi asetetaan piste P ', joka sijaitsee samalla origosta lähtevällä
säteellä kuin P siten, että pisteiden origosta mitattujen etäisyyksien tulo on = 1.
Muodosta kuvauksen komponenttifunktiot sekä laske Jacobi’n matriisi ja tämän
determinantti.
2,
missä pisteen P kuvaksi asetetaan piste P ', joka sijaitsee samalla origosta lähtevällä
säteellä kuin P siten, että pisteiden origosta mitattujen etäisyyksien tulo on = 1.
Muodosta kuvauksen komponenttifunktiot sekä laske Jacobi’n matriisi ja tämän
determinantti.
Tehtävä 133
Olkoon r avaruuden E3 paikkavektori, r tämän pituus ja r0 = r/r vastaava yksikkövektori. Osoita:a) dr = r0 . dr, b) r d(r0) = dr - (r0 . dr)r0.
4.2 Ketjusääntö
Tehtävä 134
Olkoon annettuna funktiot f : 2
2 
 3 ja g : G
3 ja g : G 
 3
3 
 :
:
f(x, y) = (xy, x + y, xey), g(x, y, z) = (y2 - 2x) ln z.
Laske yhdistetyn funktion h :  2
2 
 , h = gof, osittaisderivatta hxy(1, 0) ketjusäännön
avulla.
, h = gof, osittaisderivatta hxy(1, 0) ketjusäännön
avulla.
Tehtävä 135
Käyrät c1 ja c2 leikkaavat toisensa pisteessä P kulmassa, jonka suuruus on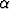 . Käyrät kuvataan käänteissäteisellä muunnoksella, jolloin saadaan käyrät d1 ja d2; nämä
leikkaavat toisensa pisteen P kuvapisteessä P '. Osoita, että myös kuvakäyrät leikkaavat
toisensa kulmassa
. Käyrät kuvataan käänteissäteisellä muunnoksella, jolloin saadaan käyrät d1 ja d2; nämä
leikkaavat toisensa pisteen P kuvapisteessä P '. Osoita, että myös kuvakäyrät leikkaavat
toisensa kulmassa 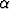 .
.
Tehtävä 136
Olkoot avaruuden E3 vektorit a ja b lineaarisesti riippumattomia. Määritellään reaaliarvoinen funktio f asettamalla
f(r) = 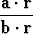 , b . r
, b . r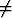 0.
0.
Määritä  f ja osoita, että funktion f derivaatta vektorin a × b suuntaan on = 0.
f ja osoita, että funktion f derivaatta vektorin a × b suuntaan on = 0.
Tehtävä 137
Avaruudessa n määriteltyä reaaliarvoista funktiota f kutsutaan p-asteiseksi
homogeenifunktioksi, jos
n määriteltyä reaaliarvoista funktiota f kutsutaan p-asteiseksi
homogeenifunktioksi, jos
f( x) =
x) =  pf(x),
pf(x), 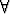


 , x
, x 
 n.
n.
Todista, että jos tällainen funktio on differentioituva, niin sille pätee Eulerin homogeenifunktiolause:
(grad f(x))x = pf(x).
4.3 Newtonin menetelmä
Tehtävä 138
Millainen kaksiulotteinen Newtonin menetelmä saadaan differentiaalin avulla yhtälöryhmän
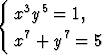
ratkaisemiseen? Esitä iteraatiokaava matriisimuodossa.
Tehtävä 139
Tutki, missä pisteissä Cartesiuksen lehden x3 + y3 = 3xy tangentin suuntakulma johonkin koordinaattiakseliin nähden on 45o. Muodosta tarvittava yhtälöryhmä ja ratkaise se kaksiulotteisella Newtonin iteraatiolla.Tehtävä 140
Muodosta Newtonin menetelmän mukainen matriisimuotoinen iteraatiokaava yhtälöparille
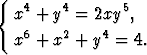
Etsi tämän avulla yksi yhtälöparin kaikkiaan neljästä (reaalisesta) ratkaisusta.
Tehtävä 141
Etsi yhtälöryhmän
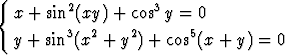
lähinnä origoa oleva ratkaisu kaksiulotteisella Newtonin iteraatiolla. Valitse lähtöarvoiksi x0 = -1, y0 = -0.5.