5 Pintateoriaa
5.1 Pintoihin liittyvät peruskäsitteet
Tehtävä 143
Olkoon f(x, y, z) = x2 - y2 + 3xz + 2. Missä pisteissä pinnan f(x, y, z) = 0 normaali on yhdensuuntainen suoran x = y = z kanssa? Laske funktion f suunnattu derivaatta origon suuntaan näissä pisteissä.Tehtävä 144
Määritä pinnan r(u, v) = u(1 + v)i + u2(1 - v)j + u3vk pisteeseen (1, 1, 0) asetetun tangenttitason yhtälö. Piirrä pinta.Tehtävä 145
Määritä pinnan r(u, v) = u cos v i + v cos u j + cos u cos v k pisteeseen (0, 0, 1) asetetun tangenttitason yhtälö. Piirrä pinta.Tehtävä 146
Määritä se pinnan r(u, v) = (u + v)i + (u2 + v2)j + (u3 + v3)k piste, jossa tangenttitaso on tason 9x + 3y - z = 0 suuntainen. Mikä on tangenttitason yhtälö?Tehtävä 147
Tutki, millaista pintaa esittää yhtälö
r(u, v) = (R + r cos u) cos v i + (R + r cos u) sin v j + r sin u k, u, v  [0, 2
[0, 2 ],
],
tarkastelemalla käyriä u = vakio, v = vakio. Laske parametriarvoja u = 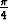 , v =
, v = 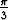 vastaava
pinnan piste ja tähän asetettu normaalivektori. Oletetaan R > r > 0. Piirrä pinta.
vastaava
pinnan piste ja tähän asetettu normaalivektori. Oletetaan R > r > 0. Piirrä pinta.
Tehtävä 148
Olkoon R > r > 0. Määritä suorakulmaiset koordinaatit niille pinnan
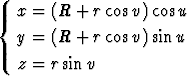
pisteille, joihin asetettu tangenttitaso on jonkin koordinaattitason suuntainen.
Tehtävä 149
Funktio f : [-1, 1] × [0, ]
] 
 2
2 
 3,
3,
f(u, v) = ((4 - u sin v) cos 2v, (4 - u sin v) sin 2v, u cos v),
määrittää erään pinnan, ns. Möbiuksen nauhan. Laske pinnan normaalivektori, ja tutki, miten sen ja xy-tason välinen kulma muuttuu, kun nauhaa pitkin kierretään ympäri. Piirrä pinta.
Tehtävä 150
Määritä pisteen a) (2, 3, 6), b) (3, 3, 1) kautta kulkeva pinnan z = xy normaali.Tehtävä 151
Tutki pinnan z =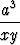 (missä a > 0) pisteeseen asetetun tangenttitason ja
koordinaattitasojen määräämän tetraedrin tilavuutta.
(missä a > 0) pisteeseen asetetun tangenttitason ja
koordinaattitasojen määräämän tetraedrin tilavuutta.
Tehtävä 152
Muodosta tangenttitason yhtälö pinnalle f(y, z) + g(z, x) + h(x, y) = 0, kun sivuamispiste on (x0, y0, z0). Funktiot oletetaan differentioituviksi.Tehtävä 153
Olkoon funktio f :

 derivoituva. Määritä pinnan
x - 2y + 3z + f(x - y + 2z) = 0 kaikkien tangenttitasojen suuntainen vektori.
derivoituva. Määritä pinnan
x - 2y + 3z + f(x - y + 2z) = 0 kaikkien tangenttitasojen suuntainen vektori.
Tehtävä 154
Olkoot dx, dy ja dz niiden pisteiden etäisyydet origosta, joissa pinnan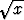 +
+ 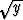 +
+ 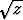 =
= 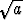 tangenttitaso leikkaa koordinaattiakselit. Laske dx + dy + dz.
tangenttitaso leikkaa koordinaattiakselit. Laske dx + dy + dz.
Tehtävä 155
Määritä käyrän
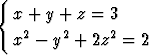
pisteeseen (1, 1, 1) asetetun normaalitason yhtälö.
Tehtävä 156
Pinnat y2 + z2 = 1 ja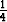 x2 + y2 - z2 = 1 leikkaavat toisensa pitkin erästä
käyrää. Tutki, missä pisteissä käyrän tangenttivektori on vaakasuora. Millainen käyrä on
kysymyksessä?
x2 + y2 - z2 = 1 leikkaavat toisensa pitkin erästä
käyrää. Tutki, missä pisteissä käyrän tangenttivektori on vaakasuora. Millainen käyrä on
kysymyksessä?
Tehtävä 157
Pinnat y2 + z2 = 1 ja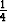 x2 + y2 - z2 = 1 leikkaavat toisensa pitkin erästä
käyrää. Laske käyrän tangenttivektori pisteessä, jonka x-koordinaatti on = 1 ja muut
koordinaatit positiivisia.
x2 + y2 - z2 = 1 leikkaavat toisensa pitkin erästä
käyrää. Laske käyrän tangenttivektori pisteessä, jonka x-koordinaatti on = 1 ja muut
koordinaatit positiivisia.
5.2 Pinnan metriikka
Tehtävä 158
Osoita, että pyörähdyspinnan r(u, v) = u cos v i + u sin v j + u2 k Gaussin kaarevuus on
K = 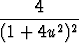 .
.
Millainen pinta on kysymyksessä?
5.3 Verhokäyristä ja -pinnoista
Tehtävä 159
Etsi mahdollinen verhokäyrä seuraaville käyräparville (parviparametrina t):a) y = (x - t)2, b) y3 = (x - t)2, c) y2 = (x - t)3, d) y = (x - t)3.
Ilmoita, milloin kyseessä todella on verhokäyrä. Piirrä kuviot.
Tehtävä 160
Suoran kulman kärki liukuu pitkin y-akselia siten, että toinen kylki kulkee pisteen (1, 0) kautta. Määritä toisen kyljen verhokäyrä ja piirrä se.Tehtävä 161
Etsi paraabeliparven tx2 - t2y - 1 = 0 (parviparametri t > 0) verhokäyrä. Piirrä kuvio paraabeleista ja verhokäyrästä.Tehtävä 162
Osoita, että vakiopituisella janalla, jonka toinen päätepiste liukuu x-akselilla ja toinen y-akselilla, on verhokäyränä asteroidi.Tehtävä 163
Osoita, että suoraa pitkin vierivän ympyrän halkaisijan verhokäyrä on sykloidi.Tehtävä 164
Etsi evoluutta seuraaville käyrille:| a) y2 = 2px; b) x = a cos u, y = b sin u (parametrina u); | |||
| c) r(t) = (cos t + t sin t)i + (sin t - t cos t)j. |