6 Käänteiskuvaukset ja implisiittifunktiot
6.1 Käänteisfunktion olemassaolo
Tehtävä 165
Määritä jokin piste, jonka ympäristössä funktiolla f : 2
2 
 2,
2,
f(x, y) = (y sin x, x + y + 1)
a) on lokaali käänteisfunktio, b) ei ole. Piirrä näiden pisteiden ympäristöön asetetun neliöruudukon kuva.
Tehtävä 166
Tutki, minkä pisteiden ympäristössä kuvauksella f : 2
2 
 2,
f(x, y) = (x3 + xy, x2/10 + y), on lokaali käänteiskuvaus. Tarkastele aluetta
{ (x, y) | -1.5 < x < 1.5, -1 < y < 1 } ja muodosta siihen piirretyn neliöruudukon kuva.
Laske funktion f Jacobi’n determinantti. Missä pisteissä tämä on = 0? Miten nämä
pisteet kuvautuvat?
2,
f(x, y) = (x3 + xy, x2/10 + y), on lokaali käänteiskuvaus. Tarkastele aluetta
{ (x, y) | -1.5 < x < 1.5, -1 < y < 1 } ja muodosta siihen piirretyn neliöruudukon kuva.
Laske funktion f Jacobi’n determinantti. Missä pisteissä tämä on = 0? Miten nämä
pisteet kuvautuvat?
Tehtävä 167
Funktio f : 2
2 
 2 määritellään asettamalla f(x, y) = ((x + y)3 + ax + ay, x - y).
Tutki lokaalin käänteisfunktion olemassaoloa tapauksissa a) a = 3, b) a = -3. Selosta,
miten funktio kuvaa xy-tason. Piirrä kuvia.
2 määritellään asettamalla f(x, y) = ((x + y)3 + ax + ay, x - y).
Tutki lokaalin käänteisfunktion olemassaoloa tapauksissa a) a = 3, b) a = -3. Selosta,
miten funktio kuvaa xy-tason. Piirrä kuvia.
Tehtävä 168
Laske funktion f : 2
2 
 2,
2,
f(x, y) = (x3 + y3, x3 - y3)
funktionaalideterminantti. Onko funktiolla globaalia käänteisfunktiota? Ratkaise (x, y) yhtälöstä (u, v) = f(x, y).
Tehtävä 169
Funktio f : 2
2 
 2, f(x1, x2) = (y1, y2), olkoon määritelty yhtälöillä
2, f(x1, x2) = (y1, y2), olkoon määritelty yhtälöillä
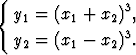
Laske funktion f Jacobi’n matriisi (funktionaalimatriisi) pisteessä (x1, x2). Osoita, että funktiolla f on käänteisfunktio g ja määritä sen lauseke. Onko funktio g kaikkialla differentioituva? Määritä funktion g Jacobi’n matriisi pisteessä (1, 8).
Tehtävä 170
Olkoon f : 2
2 
 2,
2,
f(x, y) = (ex cos y, ex sin y).
Määritä suorakulmion S = { (x, y) | r1 < x < r2, 0 < y < 2 } kuva f(S) ja tutki, onko
kuvaus f : S
} kuva f(S) ja tutki, onko
kuvaus f : S  f(S) injektio. Määritä suurin injektiivisesti kuvautuva origon
ympyräympäristö.
f(S) injektio. Määritä suurin injektiivisesti kuvautuva origon
ympyräympäristö.
Tehtävä 171
Kuvaus f : 2
2 
 2,
2,
f(x, y) = (u, v) = (ex cos y, ex sin y),
kuvaa pisteen P  (1,
(1,  /6) erään ympäristön pisteen Q
/6) erään ympäristön pisteen Q  (e
(e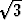 /2, e/2) eräälle ympäristölle
bijektiivisesti, jolloin on olemassa lokaali käänteiskuvaus x = g1(u, v), y = g2(u, v).
Laske funktion h(u, v) = g1(u, v)g2(u, v) osittaisderivaatat
/2, e/2) eräälle ympäristölle
bijektiivisesti, jolloin on olemassa lokaali käänteiskuvaus x = g1(u, v), y = g2(u, v).
Laske funktion h(u, v) = g1(u, v)g2(u, v) osittaisderivaatat 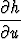 ja
ja 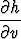 pisteessä
Q.
pisteessä
Q.
6.2 Implisiittifunktioista
Tehtävä 172
Osoita, että yhtälö x6 + 2y4 - 3x2y = 0 eräässä pisteen (1, 1) ympäristössä määrittelee funktion y = f(x). Määritä funktion kuvaajan tangentin yhtälö kyseisessä pisteessä.Tehtävä 173
Määritä Cartesiuksen lehden x3 + y3 = 3xy kaarevuussäde niissä pisteissä, missä käyrä leikkaa suoran y = x.Tehtävä 174
Yhtälö F (cx - az, cy - bz) = 0, missä F on differentioituva funktio sekä a, b ja c vakioita, määritelköön differentioituvan funktion z = f(x, y). Laske afx + bfy.Tehtävä 175
Osoita, että yhtälö sin(yz) + y2ez = x määrittelee eräässä pisteen ( 2,
2,  , 0)
ympäristössä funktion z = f(x, y). Arvioi differentiaalia käyttäen tämän funktion arvo
pisteessä (
, 0)
ympäristössä funktion z = f(x, y). Arvioi differentiaalia käyttäen tämän funktion arvo
pisteessä ( 2 + 0.01,
2 + 0.01,  - 0.03).
- 0.03).
Tehtävä 176
Funktiot F : 3
3 
 ja G :
ja G :  2
2 
 olkoot jatkuvasti derivoituvia.
Oletetaan, että yhtälöllä
olkoot jatkuvasti derivoituvia.
Oletetaan, että yhtälöllä
F (x, y, G(y, z)) = 0
on ratkaisu z = f(x, y). Lausu fx ja fy funktioiden F ja G osittaisderivaattojen avulla.
Tehtävä 177
Oletetaan, että yhtälö x = f(y, z) määrittelee funktion z = g(x, y) ainakin jossakin tarkastelupisteen (x, y, z) ympäristössä. Lausu derivaatat gx, gy ja gxy funktion f derivaattojen avulla. Oletetaan, että funktio f on riittävän monta kertaa differentioituva.Tehtävä 178
Osoita, että yhtälö x = z + y sin z eräässä origon ympäristössä määrittelee funktion z = g(x, y). Laske gxy(0, 0).Tehtävä 179
Osoita, että yhtälö yex + sin(x - y + z) = 0 määrittelee eräässä origon ympäristössä pinnan. Määritä pinnan tangenttitaso origossa.Tehtävä 180
Osoita, että yhtälöt
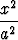 +
+ 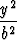 +
+ 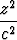 = 1 ja
= 1 ja 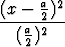 +
+ 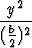 = 1
= 1
(a, b, c > 0) määrittävät käyrän pisteen (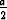 ,
,  ,
, 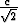 ) ympäristössä. Laske tähän pisteeseen
asetetun käyrän tangentin ja z-akselin välisen kulman kosini.
) ympäristössä. Laske tähän pisteeseen
asetetun käyrän tangentin ja z-akselin välisen kulman kosini.
Tehtävä 181
Laske funktion f(x, y, z) = xy + cos x + y2z ensimmäisen kertaluvun osittaisderivaatat ja gradientti pisteessä ( /2, 1, -
/2, 1, - /2). Mitä gradientti ilmaisee
funktiosta f ? Entä pinnasta f(x, y, z) = 0 ? Mitä osittaisderivaattojen avulla voidaan
päätellä siitä, määritteleekö yhtälö f(x, y, z) = 0 jossakin em. pisteen ympäristössä
funktiot x = x(y, z), y = y(z, x), z = z(x, y) ?
/2). Mitä gradientti ilmaisee
funktiosta f ? Entä pinnasta f(x, y, z) = 0 ? Mitä osittaisderivaattojen avulla voidaan
päätellä siitä, määritteleekö yhtälö f(x, y, z) = 0 jossakin em. pisteen ympäristössä
funktiot x = x(y, z), y = y(z, x), z = z(x, y) ?
Tehtävä 182
Osoita implisiittifunktiolauseen avulla, että yhtälöt 2x2 + 3y2 + z2 - 47 = 0 ja x2 + 2y2 - z = 0 määrittävät pisteen (-2, 1, 6) ympäristössä derivoituvat funktiot y = f(x) ja z = g(x). Laske näiden derivaatat pisteessä x = -2.Tehtävä 183
Tutki, voidaanko yhtälöistäx + y - z = 1 ja x2 + y2 - 2z = 0
ratkaista funktiot y = f(x) ja z = g(x) sopivassa pisteen (1, 1, 1) ympäristössä. Mikä on probleeman geometrinen sisältö?
Tehtävä 184
Tutki sopivaa Jacobi’n determinanttia käyttäen, voidaanko yhtälöistäx + y + z = 1 ja x2 + y2 + z2 = 1
ratkaista funktiot y = f(x) ja z = g(x) sopivassa pisteen ( ,
,  (1 +
(1 + 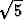 ),
),  (1 -
(1 - 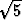 ))
ympäristössä. Mikä on probleeman geometrinen sisältö?
))
ympäristössä. Mikä on probleeman geometrinen sisältö?
Tehtävä 185
Osoita, että yhtälöty5 + xy + z2 = 4 ja exz = y2
määrittävät jossakin pisteen (3, 1, 0) ympäristössä funktiot x = f(z) ja y = g(z). Laske f' (0) ja g' (0).
Tehtävä 186
Olkoon f differentioituva funktio 2
2 
 ja olkoon (a, b, c) piste, joka
toteuttaa yhtälöt
ja olkoon (a, b, c) piste, joka
toteuttaa yhtälöt
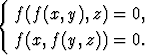
Millä funktion f osittaisderivaattoja koskevalla ehdolla yhtälöt implisiittifunktiolauseen mukaan määrittävät pisteen (a, b, c) ympäristössä funktiot x = u(z) ja y = v(z)? Merkitse osittaisderivaattoja f1 ja f2 sekä merkitse myös niiden argumentit näkyviin.
Tehtävä 187
Piste (x1, . . . , xn, y1, . . . , yp) toteuttakoon yhtälöryhmän
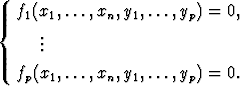
Selosta, millä ehdolla ko. pisteen ympäristössä yhtälöistä voidaan periaatteessa ratkaista riippuvuus
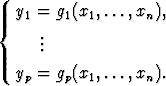
Sovella teoriaa yhtälöihin x2 + y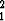 - 2y2 = 0, x + y1 - y2 - 1 = 0 pisteen (1, 1, 1)
ympäristössä.
- 2y2 = 0, x + y1 - y2 - 1 = 0 pisteen (1, 1, 1)
ympäristössä.
Tehtävä 188
Oletetaan, että yhtälö F (x, y, z) = 0 määrittää tarkastelupisteen (x0, y0, z0) eräässä ympäristössä funktiot x = x(y, z), y = y(z, x) ja z = z(x, y). Todista termodynamiikassa tarvittava yhtälö
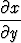
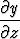
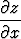 = -1.
= -1.
Tehtävä 189
Totea edellisen tehtävän yhtälön
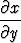
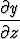
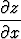 = -1
= -1
voimassaolo tapauksessa F (x, y, z) = x3y2z - 1, ts. muodosta funktiot x, y, z, laske näistä tarvittavat osittaisderivaatat ja niiden tulo.
6.3 Sidotut ääriarvot
Tehtävä 190
Etsi pisteen (a, 0) lyhin etäisyys paraabelista y2 = 4x käyttämällä Lagrangen kertoimia.Tehtävä 191
Etsi origon lyhin etäisyys hyperbelistä x2 + 8xy + 7y2 = 45 käyttäen Lagrangen kertoimia.Tehtävä 192
Määritä origon suurin ja pienin etäisyys käyrästä
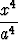 +
+ 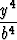 = 1.
= 1.
Tehtävä 193
Määritä se ellipsin
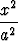 +
+ 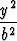 = 1
= 1
ensimmäisessä neljänneksessä oleva piste, johon asetettu tangentti muodostaa koordinaattiakseleiden kanssa mahdollisimman pienialaisen kolmion.
Tehtävä 194
Olkoot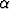 ,
, 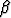 ja
ja 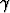 kolmion kulmat. Etsi suurin arvo lausekkeelle
sin
kolmion kulmat. Etsi suurin arvo lausekkeelle
sin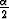 sin
sin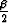 sin
sin 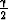 .
.
Tehtävä 195
Puolisuunnikkaan sivut b ja d ovat yhdensuuntaiset, sivut a ja c yhtä pitkät; puolisuunnikkaan ala on annettu. Määritä suhde a : b : c : d siten, että summa a + b + c on mahdollisimman pieni.Tehtävä 196
Pisteen P (a, b, c) kaikki koordinaatit ovat positiivisia. Määritä pisteen
kautta kulkevan tason ja kaikkien koordinaattitasojen rajoittaman tetraedrin pienin
mahdollinen tilavuus.
(a, b, c) kaikki koordinaatit ovat positiivisia. Määritä pisteen
kautta kulkevan tason ja kaikkien koordinaattitasojen rajoittaman tetraedrin pienin
mahdollinen tilavuus.
Tehtävä 197
Suuntaissärmiön särmien pituuksien summa olkoon 12a. Määritä särmiön suurin mahdollinen tilavuus.Tehtävä 198
Halutaan rakentaa suorakulmaisen särmiön muotoinen laatikko, jonka tilavuus a3 on annettu. Laatikon pohja ja sivuseinät ovat puuta ja kansi lasia. Kuinka särmien pituudet on valittava, jotta hinta olisi mahdollisimman alhainen, kun lasi on kaksi kertaa niin kallista kuin puu?Tehtävä 199
Määritä funktion f(x, y, z) = x3 + y3 + z3 suurin ja pienin arvo tason x + y + z = 3 ja pallon x2 + y2 + z2 = 27 leikkausympyrällä.Tehtävä 200
Määritä Lagrangen kertojaa käyttäen funktion f(x1, . . . , xn) = (x1. . . xn)2 suurin arvo yksikköpallolla x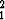 + . . . x
+ . . . x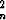 = 1. Päättele tuloksesta aritmeettisen ja
geometrisen keskiarvon välinen epäyhtälö
= 1. Päättele tuloksesta aritmeettisen ja
geometrisen keskiarvon välinen epäyhtälö 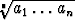 <
< 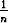 (a1 + . . . + an), missä
ak > 0.
(a1 + . . . + an), missä
ak > 0.
Tehtävä 201
Etsi lausekkeen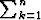 x
x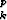 ääriarvot, kun side-ehtona on
ääriarvot, kun side-ehtona on 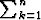 xk = a.
xk = a.