7 Taso- ja avaruusintegraali
7.1 Tasointegraalin määrittely
Tehtävä 205
Tarkastellaan funktiota f(x, y) = x + y neliössä { (x, y) | 0 < x < 1, 0 < y < 1 }. Neliö jaetaan suorilla x = a ja y = b neljään osasuorakulmioon; 0 < a < 1, 0 < b < 1. Muodosta tähän jakoon p liittyvä alasumma Sp ja yläsumma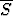 p . Määritä suppSp ja
infp
p . Määritä suppSp ja
infp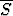 ptällaisille jaoille. Seuraako lukujen erisuuruudesta, että funktio ei ole integroituva
ko. neliössä?
ptällaisille jaoille. Seuraako lukujen erisuuruudesta, että funktio ei ole integroituva
ko. neliössä?
Tehtävä 206
Olkoot T1 ja T2 kaksi perussuorakulmiota, joille pätee A T1, A
T1, A  T2.
Osoita, että jos funktion f nollajatko f
T2.
Osoita, että jos funktion f nollajatko f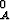 on integroituva yli joukon T1, niin se on
integroituva myös joukon T2 yli ja integraalit ovat yhtä suuret:
on integroituva yli joukon T1, niin se on
integroituva myös joukon T2 yli ja integraalit ovat yhtä suuret:
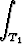 f
f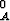 =
= 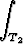 f
f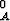 .
.
7.2 Tasointegraalin perusominaisuudet
Tehtävä 207
Todista suoraan integraalin määritelmään perustuen tasointegraalin ominaisuus
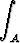
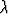 f =
f = 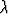
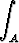 f,
f,
missä 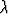 on vakio.
on vakio.
Tehtävä 208
Todista funktioiden nollajatkoille: (f + g)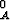 = f
= f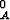 + g
+ g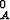 .
.
Tehtävä 209
Olkoon joukko A jaettu kahteen osaan A = A1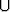 A2, missä A1
A2, missä A1 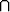 A2 = Ø.
Osoita: f
A2 = Ø.
Osoita: f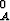 = f
= f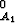 + f
+ f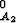 .
.
Tehtävä 210
Osoita vastaesimerkillä, että tasointegraalin väliarvolauseen oletusta integrointijoukon A yhtenäisyydestä ei voida jättää pois.7.3 Tasointegraalin laskeminen
Tehtävä 211
Funktio f(x, y) olkoon jatkuva joukossa { (x, y) | a1 < x < a2, b1(x) < y < b2(x) }, missä funktiot b1(x) ja b2(x) ovat jatkuvia välillä [a1, a2]. Todista, että funktio
g(x) = 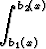 f(x, y) dy
f(x, y) dy
on jatkuva välillä [a1, a2].
Tehtävä 212
Laske
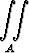 fxy(x, y) dxdy,
fxy(x, y) dxdy,
kun A on suorakulmio [a, b] × [c, d].
Tehtävä 213
Laske seuraavat integraalit:a) 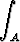 x2 da, A = { (x, y) | |x| + |y| < 1 }; x2 da, A = { (x, y) | |x| + |y| < 1 }; | |||
b) 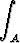  da, A = { (x, y) | |x| < 1, 1 < y < 2 }. da, A = { (x, y) | |x| < 1, 1 < y < 2 }. |
Tehtävä 214
Laske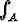 xy da, kun A on a) kolmio, jonka kärjet ovat (0, 0), (1, 1), (1, 2);
b) kuvio, jonka määrittelevät ehdot x
xy da, kun A on a) kolmio, jonka kärjet ovat (0, 0), (1, 1), (1, 2);
b) kuvio, jonka määrittelevät ehdot x  [0, 1], 0 < y <
[0, 1], 0 < y < 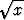 ; c) segmentti, jota rajoittavat
suora y = 2(x - p) ja paraabeli y2 = 2px.
; c) segmentti, jota rajoittavat
suora y = 2(x - p) ja paraabeli y2 = 2px.
Tehtävä 215
Etsi funktion f : 2
2 
 ,
,
f(x, y) = 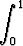
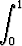 (10 - xu - yv2)2 dudv,
(10 - xu - yv2)2 dudv,
suhteelliset ääriarvot. Ovatko nämä maksimeja vai minimejä?
Tehtävä 216
Laske integraali
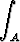
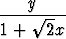 dxdy, A = { (x, y) | 0 < x < y <
dxdy, A = { (x, y) | 0 < x < y < 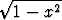 }.
}.
7.4 Avaruusintegraali
Tehtävä 217
Olkoon V = { (x, y, z) | x > 0, y > 0, z > 0, x + y + z < 1 }. Laske a)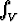 (1 - x - y)5 dv, b)
(1 - x - y)5 dv, b) 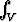 xyz4 dv.
xyz4 dv.
Tehtävä 218
Tutki, millä muuttujan t arvoilla funktio
f(t) = 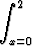
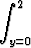
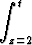 xy(z - 1) ln(1 + z4) dxdydz
xy(z - 1) ln(1 + z4) dxdydz
saa pienimmän arvonsa.
7.5 Muuntaminen sijoituksella
Tehtävä 219
Laske integraali
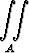 (x + 2y)4(x - 2y)6 dxdy,
(x + 2y)4(x - 2y)6 dxdy,
kun integroimisjoukkona on tasoalue A = { (x, y) | |x + 2y| < 1, |x - 2y| < 2 }.
Tehtävä 220
Laske sopivan muuttujanvaihdon avulla integraali
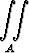 (2x + 3y)2(x - 5y)2 dxdy, missä A = { (x, y) | |2x + 3y| < 4, |x - 5y| < 3 }.
(2x + 3y)2(x - 5y)2 dxdy, missä A = { (x, y) | |2x + 3y| < 4, |x - 5y| < 3 }.
Tehtävä 221
Laske käyrien y3 = ax2, y3 = bx2, x4 = cy3, x4 = dy3 (0 < a < b, 0 < c < d) ensimmäisessä neljänneksessä rajoittaman alueen pinta-ala. Valitse uusiksi muuttujiksi u ja v, jotka määräytyvät yhtälöistä y3 = ux2, x4 = vy3.Tehtävä 222
Laske muotoa x = as cos t, y = bs sin t (a ja b vakioita) olevaa muunnosta käyttäen tasointegraali
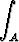 ln
ln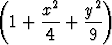 da, A = { (x, y) | x > 0, y > 0, 9x2 + 4y2 < 36 }.
da, A = { (x, y) | x > 0, y > 0, 9x2 + 4y2 < 36 }.
Tehtävä 223
Laske sen kappaleen tilavuus, jota rajoittavat xy-tason yläpuolella pinnat| a) x2 + y2 = a2, x2 + y2 = az, z = 0 (a > 0); | |||
| b) z = x2 - y2, x2 + y2 = 1, z = 0. |
Tehtävä 224
Laske sen kappaleen tilavuus, jota rajoittavat paraboliset lieriöt z2 = y, z2 = 2y, x2 = z, x2 = 2z, y2 = x, y2 = 2x. Siirry aluksi yhtälöiden x = uy2, y = vz2, z = wx2 määräämiin uusiin muuttujiin u, v, w.Tehtävä 225
Laske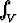 x2y dv, kun V = { (x, y, z) | z2 < x2 + y2 < 1 }.
x2y dv, kun V = { (x, y, z) | z2 < x2 + y2 < 1 }.
Tehtävä 226
Laske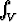 xyz dv, kun V on pallon oktantti
xyz dv, kun V on pallon oktantti
{ (x, y, z) | x2 + y2 + z2 < 1, x > 0, y > 0, z > 0 }.
Tehtävä 227
Muunna integraali
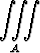 f(x, y, z) dxdydz
f(x, y, z) dxdydz
pallokoordinaatteihin, kun funktio f oletetaan integroituvaksi ja integroimisjoukko A on R-säteinen origokeskinen pallo. Laske sovellutuksena R-säteisen pallon tilavuus.
Tehtävä 228
Laske sekä pallon x2 + y2 + z2 = R2 että kartion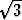 z =
z = 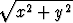 sisään jäävän avaruuden osan tilavuus avaruusintegraalina siirtymällä a) lieriö-,
b) pallokoordinaatistoon.
sisään jäävän avaruuden osan tilavuus avaruusintegraalina siirtymällä a) lieriö-,
b) pallokoordinaatistoon.
Tehtävä 229
Pisteen P0 r0 keskietäisyys kappaleen B pisteistä on integraali
r0 keskietäisyys kappaleen B pisteistä on integraali
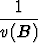
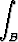 |r - r0| dv.
|r - r0| dv.
Laske pisteen (0, 0, c) keskietäisyys pallon r < R pisteistä, kun c > R.
Tehtävä 230
Laske pallokoordinaateissa integraali
f(t) = 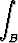
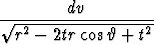 , t > 0,
, t > 0,
missä B on origokeskinen R-säteinen pallo. Piirrä funktion f kuvaaja.
Tehtävä 231
Laske tasa-arvokäyrien avulla integraali
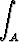 sin(x2 + y2) dxdy, A = { (x, y) | 1 < x2 + y2 < 4 }.
sin(x2 + y2) dxdy, A = { (x, y) | 1 < x2 + y2 < 4 }.
Tehtävä 232
Anna differentiaaligeometrinen perustelu a) lieriökoordinaatiston tilavuusalkiolle dv = d
d d
d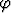 dz, b) pallokoordinaatiston tilavuusalkiolle dv = r2 sin
dz, b) pallokoordinaatiston tilavuusalkiolle dv = r2 sin 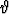 drd
drd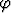 d
d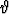 .
.
7.6 Integraali avaruudessa  n
n
Tehtävä 233
Olkoon Bn(r) avaruuden n r-säteinen pallo:
n r-säteinen pallo:
Bn(r) = { x 
 n | ||x|| < r }.
n | ||x|| < r }.
Olkoon 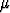 (Bn (r)) tämän mitta (pituus, pinta-ala, tilavuus, etc.). Johda yksikköpallojen
Bn (1) = Bn mitoille seuraava rekursio:
(Bn (r)) tämän mitta (pituus, pinta-ala, tilavuus, etc.). Johda yksikköpallojen
Bn (1) = Bn mitoille seuraava rekursio:
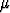 (B1) = 2,
(B1) = 2, 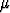 (B2) =
(B2) =  ,
, 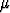 (Bn) =
(Bn) = 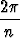
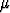 (Bn-2), n = 3, 4, . . . .
(Bn-2), n = 3, 4, . . . .