8 Sovellutuksia

8.1 Pinta-alan ja tilavuuden laskeminen

Tehtävä 235

Laske sen kappaleen tilavuus, jota rajoittavat pinnat z = xy, x = y², z = 0, x = 1. (Kappale sijaitsee oktantissa x > 0, y > 0, z > 0.)

Vastaus

Tehtävä 236

Laske sen kappaleen tilavuus, jota rajoittavat pinnat z = xye^y, z = 0, x + y = 1.

Tehtävä 237

Laske sen kappaleen tilavuus, jota rajoittavat pinnat

x = 0, x = 2, y = 0, y = 1, z = 0, z = 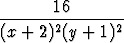16
-------2-------2
(x + 2) (y + 1) .

Tehtävä 238

Laske sen kappaleen massa, jota xy-tason yläpuolella rajoittavat pinnat z = 0, z = x² - y², x² + y² = 1 ja jonka massatiheys on verrannollinen z-koordinaattiin.

Tehtävä 239

Laske sen kappaleen massa, jota rajoittavat pinnat x = 0, y = 0, z = 4 ja z = e^x+y ja jonka massatiheys on

= 1/z.

8.2 Keskiö ja hitausmomentti

Tehtävä 240

Olkoon f(x) < g(x) välillä x

[a, b]. Kirjoita levyn

{ (x, y) | f(x) < y < g(x), a < x < b }

keskiön koordinaatit (massakeskipisteen koordinaatit, jos levy oletetaan homogeeniseksi) kaksinkertaisina integraaleina ja sievennä nämä mahdollisimman pitkälle.

Tehtävä 241

Ympyränsektorin keskuskulma on 2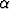

. Laske sektorin keskiö.

Tehtävä 242

Ympyräalueen neljännekselle { (x, y) | x > 0, y > 0, x² + y² < R } on levitetty massa, jonka pintatiheys on

(x, y) = x. Etsi massakeskipiste.

Tehtävä 243

Käyrät y = x^k ja x = y^k (k > 0, k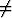

1) rajoittavat tasoalueen ensimmäisessä neljänneksessä. Laske tämän keskiö. Miten keskiö käyttäytyy, kun k -->

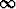Tehtävä 244

Olkoon k > 0. Määritä tasoalueen

G = { (x, y) | x⁴ < y < 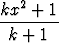kx2 + 1
--------
k + 1 }

keskiö ja tutki, millä parametrin k arvoilla se ei kuulu alueeseen G.

Tehtävä 245

Etsi suorakulmion [0, a] × [0, b] massakeskipiste, kun massan pintatiheys on

(x, y) = y.

Tehtävä 246

Määritä sen tasokuvion keskiö, jota rajoittavat x-akseli ja sykloidin kaari

r(t) = a(t - sin t)i + a(1 - cos t)j, t [0, 2].

Tehtävä 247

Laske ellipsialueen neljänneksen (rajoina pääakselit) keskiö.

Tehtävä 248

Laske suorakulmion hitausmomentti keskipisteen suhteen.

Tehtävä 249

Määritä paraabelien y² = x + 1 ja 4y² = x + 4 reunustaman äärellisen tasokuvion keskiö sekä hitausmomentit koordinaattiakselien ja origon suhteen.

Tehtävä 250

Neljännesympyrän { (x, y) | x² + y² < R², x > 0, y > 0 } muotoisella levyllä on massatiheys

(x, y) = x. Laske levyn massakeskipiste.

Tehtävä 251

Laske Guldinin säännöllä keskiö ympyrärenkaan puolikkaalle:

{ (x, y) | b² < x² + y² < a², y > 0 }.

Tehtävä 252

Kirjoita kaavat pyörähdyksestä x-akselin ympäri muodostuneen kappaleen keskiön koordinaateille yhden muuttujan integraalina. Laske erityisesti pyörähdyskartion keskiö.

Tehtävä 253

Ympyrän y² + z² = R², x = a jokaisesta pisteetä asetetaan normaali z-akselille. Nämä muodostavat pinnan, jota kutsutaan konoidiksi. Laske konoidin ja em. ympyrän tason rajoittaman kappaleen tilavuus ja keskiö.

Tehtävä 254

Pyramidissa, jota reunustavat tasot x = 0, y = 0, z = 0, x + y + z = a, on massatiheys

(x, y, z) = z. Laske massakeskipiste. Oletetaan a > 0.

Tehtävä 255

Kolmion sivun pituus on b ja vastaava korkeus h. Laske kolmion hitausmomentti sivun suhteen.

Tehtävä 256

Laske ellipsin muotoisen homogeenisen levyn hitausmomentti keskipisteen kautta kulkevan levyä vastaan kohtisuoran akselin suhteen.

Tehtävä 257

Homogeenisen suorakulmaisen särmiön sivujen pituudet ovat a, b ja c sekä kokonaismassa m. Laske hitausmomentti ja hitaussäde särmän suhteen.

Tehtävä 258

Homogeenisen prisman kokonaismassa on m. Sen kohtisuora poikkileikkaus on tasakylkinen suorakulmainen kolmio, jonka kateetin pituus on a. Prisman korkeus on c. Laske prisman hitausmomentit sivusärmien (pituudeltaan c) suhteen.

Tehtävä 259

Homogeenisen tetraedrin kokonaismassa on m ja sitä rajoittavat koordinaattitasot ja taso x/a + y/b + z/c = 1, missä a > 0, b > 0, c > 0. Laske kappaleen hitausmomentti ja hitaussäde z-akselin suhteen.

Tehtävä 260

Lieriön muotoista kappaletta rajoittavat pinnat y² + z² = 1, x = 0 ja x = 1. Kappaleen tiheys on

(x, y, z) = 1 + x². Laske kokonaismassa, massakeskipiste ja hitausmomentti symmetria-akselin suhteen.

Tehtävä 261

Etsi homogeenisen pallon oktantin keskiö.

Tehtävä 262

Etsi puolipallon massakeskipiste, kun tiheys on suoraan verrannollinen etäisyyteen keskipisteestä.

Tehtävä 263

Määritä R-säteisen puolipallon massakeskipiste, kun tiheys pallokoordinaateissa on

(r, , ) = k
------
r + R 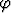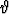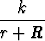(k vakio).

Tehtävä 264

Pallon kokonaismassa on m, säde R ja tiheys suoraan verrannollinen keskipisteestä laskettuun etäisyyteen (verrannollisuuskertoimena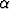

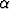r. Laske pallon hitausmomentti J keskipisteen kautta kulkevan akselin suhteen. Laske myös hitaussäde r₀, so. esitä hitausmomentti muodossa J = mr

Vastaus

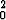Tehtävä 265

Laske homogeenisen suoran ympyrälieriön (korkeus = h, pohjan säde = r) hitausmomentti a) lieriön akselin, b) pohjan halkaisijan suhteen. Lausu tulos lieriön kokonaismassan m =

r²h avulla. (Massa = tilavuus, koska homogeenisen kappaleen massatiheydeksi voidaan ottaa 1.)

Tehtävä 266

Laske homogeenisen suoran pyörähdyskartion (korkeus h, pohjan säde r) toinen momentti akselin kautta kulkevan tason suhteen ja pohjatason suhteen. Laske näiden avulla kappaleen hitausmomentit akselin ja pohjan halkaisijan suhteen. Lausu nämä kappaleen kokonaismassan avulla.

Tehtävä 267

Laske homogeenisen pyörähdysellipsoidin hitausmomentti pyörähdysakselin suhteen. Lausu tulos kappaleen kokonaismassan avulla.

Tehtävä 268

Kappale sijaitsee xy-tason yläpuolella; sitä rajoittaa ylhäältä pyörähdysparaboloidi z = 2 - x² - y² ja alhaalta pyörähdyskartio z² = x² + y². Laske lieriökoordinaattien avulla kappaleen tilavuus, keskiö ja hitausmomentti z-akselin suhteen.

Tehtävä 269

Laske homogeenisen R-säteisen pallon hitausmomentti suoraan integroimalla a) halkaisijan, b) palloa sivuavan suoran suhteen. Lausu tulokset pallon kokonaismassan avulla.

Tehtävä 270

Todista Guldinin ensimmäinen sääntö: Jos tasokuvio pyörähtää samassa tasossa olevan akselin ympäri, joka ei leikkaa kuviota, niin syntyvän pyörähdyskappaleen tilavuus on kuvion pinta-ala kerrottuna kuvion keskiön kulkemalla matkalla.