9 Epäoleelliset integraalit; integraalin derivointi parametrin suhteen
9.1 Epäoleelliset taso- ja avaruusintegraalit
Tehtävä 271
Olkoon A = { (x, y) | x > 0, y > 0 }. Osoita hajaantuminen tai laske arvo epäoleelliselle tasointegraalille
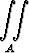 (x + y)e-x-y dxdy.
(x + y)e-x-y dxdy.
Tehtävä 272
Olkoon a > 0, b > 0, A = { (x, y) | x > 0, y > 0 }. Laske epäoleellinen integraali
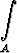 e-(ax+by)2
da
e-(ax+by)2
da
sijoituksella u = ax + by, v = y/x.
Tehtävä 273
Tutki, onko seuraava epäoleellinen integraali olemassa:
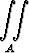
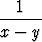 dxdy, A = { (x, y) | 0 < x < 1, 0 < y < 1 }.
dxdy, A = { (x, y) | 0 < x < 1, 0 < y < 1 }.
Tehtävä 274
Olkoon A = { (x, y) | x2 + y2 < 1 }. Laske arvo tai osoita hajaantuminen tasointegraaleille
a) 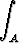 ln
ln 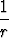 da, b)
da, b) 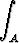
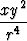 da; r =
da; r = 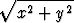 .
.
Tehtävä 275
Millä kokonaislukuarvoilla p avaruusintegraali
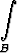
 dv
dv
suppenee, kun B on yksikköpallo { (x, y, z) | x2 + y2 + z2 < 1 }? Tässä on
r = 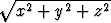 .
.
Tehtävä 276
Laske epäoleelliset integraalit
a) 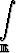 e-x2
dx, b)
e-x2
dx, b)
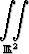 e-x2-y2
dxdy, c)
e-x2-y2
dxdy, c) 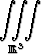 e-x2-y2-z2
dxdydz.
e-x2-y2-z2
dxdydz.
Tehtävä 277
Laske arvo tai osoita hajaantuminen tasointegraalille
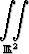
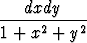 .
.
Tehtävä 278
Laske arvo tai osoita hajaantuminen avaruusintegraalille
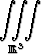
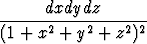 .
.
Tehtävä 279
Olkoon f : 2
2 
 koko tasossa jatkuva ja rajoitettu funktio. Olkoon
olemassa vakiot a, c ja
koko tasossa jatkuva ja rajoitettu funktio. Olkoon
olemassa vakiot a, c ja 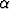 > 2 siten, että
> 2 siten, että
r > a 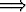 0 < f(x, y) <
0 < f(x, y) < 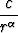 ,
,
missä r = 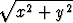 . Osoita, että epäoleellinen integraali
. Osoita, että epäoleellinen integraali 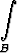 2f suppenee.
2f suppenee.
Tehtävä 280
Olkoon funktio f : A
 2
2 
 jatkuva ja rajoitettu mitallisessa joukossa A
paitsi pisteessä (x0, y0)
jatkuva ja rajoitettu mitallisessa joukossa A
paitsi pisteessä (x0, y0)  A. Olkoon edelleen olemassa vakiot c ja
A. Olkoon edelleen olemassa vakiot c ja 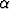 < 2 siten,
että
< 2 siten,
että
0 < f(x, y) < ![------------c------------
[(x - x0)2 + (y - y0)2]a/2](kuvat/va334x.gif)
muualla paitsi pisteessä (x0, y0). Osoita, että epäoleellinen integraali 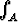 f suppenee.
f suppenee.
9.2 Integraalin derivointi parametrin suhteen
Tehtävä 281
Muodosta seuraavat derivaatat laskematta integraalia ensin:
a) 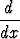
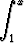 t dt, b)
t dt, b) 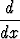
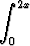
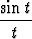 dt, c)
dt, c) 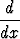
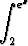
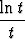 dt.
dt.
Tarkista tulos integroimalla ensin ja sen jälkeen derivoimalla, mikäli mahdollista.
Tehtävä 282
Muodosta
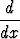
 ln(1 + tx) dt
ln(1 + tx) dt
a) derivoimalla integraalimerkin alla, b) integroimalla ensin.
Tehtävä 283
Olkoon
f(x) = 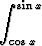
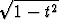 dt, x
dt, x 
 .
.
Laske f' (x) välillä [0, 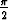 ]. Esitä funktiolle f yksinkertaisempi lauseke tällä välillä
laskematta eo. integraalia. Onko funktio koko reaaliakselilla jaksollinen? Piirrä funktion
kuvaaja.
]. Esitä funktiolle f yksinkertaisempi lauseke tällä välillä
laskematta eo. integraalia. Onko funktio koko reaaliakselilla jaksollinen? Piirrä funktion
kuvaaja.
Tehtävä 284
Funktio f määritellään asettamalla
f(t) = 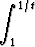
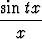 dx, t > 0.
dx, t > 0.
Laske f' (t).
Tehtävä 285
Olkoon x > -1. Laske integraali
f(x) = 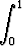 tx dt
tx dt
ja derivoi saatu yhtälö puolittain muuttujan x suhteen n kertaa.
Tehtävä 286
Millä muuttujan t arvolla funktio
f(t) = 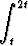 e-x2
dx
e-x2
dx
saa suurimman arvonsa?
Tehtävä 287
Yhtälö
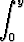 et dt +
et dt + 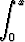 sin t dt = 0
sin t dt = 0
määrittelee funktion y(x). Lausu implisiittistä derivointia käyttäen integraaleja laskematta y' (x) muuttujien x ja y avulla.
Tehtävä 288
Laske f'(x), kun
a) f(x) = 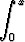 ext2
dt, b) f(x) =
ext2
dt, b) f(x) = 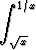 cos(xt2) dt (x > 0).
cos(xt2) dt (x > 0).
Tehtävä 289
Olkoon
F (s) = 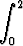
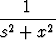 dx, s > 0.
dx, s > 0.
Laske integraali. Totea, että integraalimerkin alla derivoimisen edellytykset ovat voimassa ja laske derivaatta F '(s) sekä integraalimerkin alla derivoimalla että suoraan laskemastasi lausekkeesta. Miten tulosta voidaan käyttää integraalin
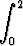
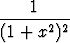 dx
dx
laskemiseen?
Tehtävä 290
Funktion
F (s) = 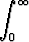 f(s, t) dt, missä f(s, t) = s3e-s2t,
f(s, t) dt, missä f(s, t) = s3e-s2t,
derivaattaa F '(0) ei voida laskea derivoimalla integraalimerkin alla. Totea, että asiaa koskevan lauseen oletukset eivät ole voimassa: ei ole olemassa sellaista funktiota g(t), että
|fs(s, t)| < g(t)  s
s  [-1, 1] ja
[-1, 1] ja 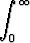 g(t) dt <
g(t) dt < 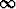 .
.
Tehtävä 291
Määritä funktion
F (s) = 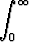 e-st dt, s > 0,
e-st dt, s > 0,
kaikkien kertalukujen derivaatat derivoimalla integraalimerkin alla. Miksi derivointi on sallittua? Johda derivaattojen avulla tulos
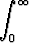 tne-t dt = n!, n
tne-t dt = n!, n 
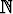 .
.
Tehtävä 292
Gammafunktio määritellään integraalilla
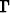 (x) =
(x) = 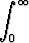 tx-1e-t dt, x > 0.
tx-1e-t dt, x > 0.
Mitä edellinen tehtävä kertoo gammafunktion arvoista, kun argumenttina on luonnollinen luku? Piirrä gammafunktion kuvaaja. Tarkastele tällöin myös negatiivisia muuttujan arvoja; funktio määritellään näillä arvoilla muulla tavoin kuin em. integraalilla.