11 Pintaintegraali

11.1 Määrittely ja laskeminen

Tehtävä 316

Laske lieriön x² + y² = 1 satulapinnasta z = xy erottaman osan pinta-ala.

Vastaus

Tehtävä 317

Laske sen pinnan ala, jonka lieriö x² + y² = R² leikkaa a) kartiosta z =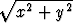 V~ 22
x+y

, b) elliptisestä paraboloidista z = 2 - 1
2

(x² + y²).

Vastaus

Tehtävä 318

Laske ns. Viviani’n ikkunan pinta-ala, so. sen pinnanpalan ala, jonka lieriö x² + y² = Rx erottaa pallosta x² + y² + z² = R².

Tehtävä 319

Laske paraboloidin z = x² + y² ja kartion z² = x² + y² rajoittaman kappaleen kokonaispinta-ala.

Vastaus

Tehtävä 320

Pinnanpala on annettu parametriesityksen avulla: x = 8u², y = v², z = 4uv, u

[0, 1], v

[0, 3]. Laske pinnanpalan ala.

Vastaus

Tehtävä 321

Laske pintaintegraali

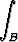integral

B x² dS, B = { (x, y, z) | x² + y² = 1, 0 < z < 1 }.

Vastaus

Tehtävä 322

Laske R-säteisen pallon tilavuus ja pinta-ala suorittamalla integroinnit pallokoordinaateissa.

11.2 Sovellutuksia

Tehtävä 323

Laske puolipallon pinnan keskiö.

Tehtävä 324

Pallopinnan säde on R ja pinnalla on tasainen massajakauma, jonka kokonaismassa on m. Laske pallopinnan hitausmomentti keskipisteen kautta kulkevan akselin suhteen.

Tehtävä 325

Laske homogeenisen umpinaisen pallon ja homogeenisen pallokuoren hitausmomentit keskipisteen kautta kulkevan akselin suhteen, kun pallon säde R ja (koko pallon tai kuoren) kokonaismassa m.

Tehtävä 326

Kuinka monta prosenttia maapallon pinta-alasta sijaitsee kääntöpiirien välissä? Entä napa-alueilla, so. napapiirien sisäpuolella? Muodosta tarvittavat pintaintegraalit pallokoordinaateissa ja laske ne. Anna vastaus prosenttiyksikön tarkkuudella. (Kääntöpiirien leveysasteet ovat ±

ja napapiirien ±(90^o -

), missä

= 23.5^o .)

Tehtävä 327

Homogeeninen pallokuori leikataan kahdella yhdensuuntaisella tasolla. Osoita, että tasojen väliin jäävän pallonpintavyöhykkeen keskiö sijaitsee tasojen keskivälillä.