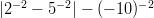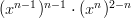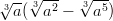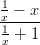Potenssit ja juuret

Potenssi an tarkoittaa tuloa, jossa on n yhtä suurta tekijää, jokainen = a. Tällöin siis n on luonnollinen luku ja a voi olla mikä tahansa luku. Vaiheittain määritelmä laajennetaan koskemaan kaikkia reaalilukuja n. Tällöin joudutaan rajoittumaan positiivisiin lukuihin a.
 Kokonaislukupotenssit
Kokonaislukupotenssit Murtopotenssit
Murtopotenssit Irrationaalinen potenssi
Irrationaalinen potenssi
Jos luvulla x on ominaisuus xn = a, sanotaan, että x on luvun a n:s
juuri ja merkitään x = 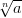 . Jos a > 0 ja n on parillinen, löytyy
lukua a vastaamaan kaksi lukua x, toinen positiivinen, toinen negatiivinen.
Positiivista kutsutaan juuren päähaaraksi.
. Jos a > 0 ja n on parillinen, löytyy
lukua a vastaamaan kaksi lukua x, toinen positiivinen, toinen negatiivinen.
Positiivista kutsutaan juuren päähaaraksi.
Korottamalla yhtälö xn = a potenssiin 1∕n saadaan potenssin laskusääntöjen mukaan x = a1∕n, mikä siis on toinen tapa merkitä juurta. Tämän tulkitaan yleensä tarkoittavan päähaara-arvoa.
Potenssin ja juuren määritelmät voidaan laajentaa myös tapaukseen, jossa a on negatiivinen luku tai kompleksiluku; myös n voi olla kompleksiluku. Tilanteesta tulee tällöin kuitenkin huomattavasti monimutkaisempi.
Esimerkiksi: 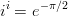 (!)
(!)

Esimerkkejä
- Erilaisten potenssi- ja juurifunktioiden kuvaajia:
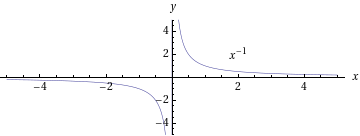
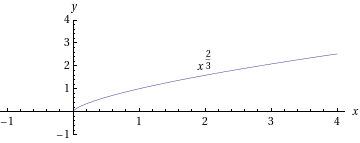
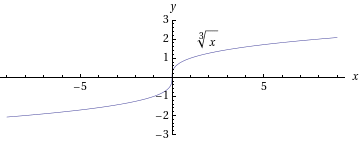

- Sievennetään käyttäen potenssin laskusääntöjä:
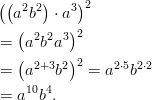
- Sievennetään murtopotenssien tulo käyttämällä potenssien ja
murtolukujen laskusääntöjä:
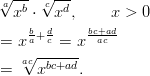
(LiveGr3D)
Potenssifunktion kuvaaja

Harjoitustehtäviä
- Laske:
-
- Laske:
-
- Laske:
-
- Sievennä:
-
Tehtävien vastaukset:

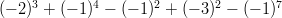
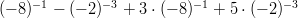
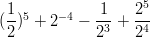

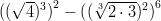
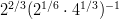

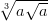

![2 1 1 [(− -)3 − (− 1 -)−3] : (− 4-) 3 2 3](potenssitjajuuret12x.gif)