| Sanna Ranto, LUKUTEORIA JA ALGEBRA Versio 1, 1.11.2003 | LINEAARIALGEBRA |
Matriisitulon determinantti
Identiteettimatriisin In determinantti on selvästi 1 kaikilla arvoilla n.
Olkoot A = (aij) ja B = (bij) kaksi (n × n)-matriisia.
Lause. det(AB) = det A det B.
Todistus. Esitetään matriisi A käyttäen sen pystyrivejä: A = (A(1),...,A(n)). Matriisitulon määritelmän mukaan tulo AB voidaan esittää käyttäen pystyrivejä:

Täten

Jos ylläolevassa summassa ih = ik, niin determinantissa det(Ai1,...,Ain) on kaksi samaa saraketta ja se on ominaisuuden (D5) ja sivun Transponoidun matriisin determinantti huomautuksen nojalla nolla. Täten summaan jää käsiteltäväksi vain ne summan alkiot, joissa indekseissä i1 ,i2,...,in esiintyy kukin luku 1, 2,...,n tarkalleen yhden kerran, toisin sanoen (i1 , i2 , ... , in ) käy läpi kaikki lukujen 1, 2,...,n permutaatiot.
Täten determinantin ominaisuuden (D4) nojalla, kun tehdään riittävän monta peräkkäistä sarakkeen vaihtoa, saadaan

Olkoon J kaikkien permutaatioiden (j1,...jn) joukko. Silloin
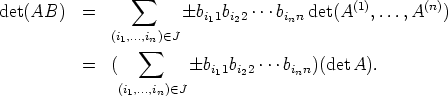

Nyt siis det (AB) = det A det B. ![[]](images/msam10-c-3.gif)
Linkit:
Determinantin perusominaisuuksia
Yksinkertaisia matriiseja
Matriisitulo
Transponoidun matriisin determinantti