Jäännösluokkarengas

Ryhmälle (G,*) määriteltiin normaalin aliryhmän (N,*) avulla tekijäryhmä G/N. Vastaavasti määritellään nyt renkaalle (R, +, ^. ) jäännösluokkarengas R/I renkaan ihanteen I avulla.

Olkoon I renkaan (R, +, ^. ) ihanne. Silloin ryhmä (I, +) on ryhmän (R, +) normaali aliryhmä – normaalisuus seuraa ryhmän (R, +) kommutatiivisuudesta. Täten voidaan muodostaa tekijäryhmä

missä D on jokin jäännösluokkien a + I edustajisto. Tekijäryhmän operaatio + määritellään luonnollisesti kaikille a,b D :

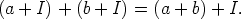
Lause. Jos I on renkaan (R, +, ^. ) ihanne, niin (R/I, +, ^. ) on rengas seuraavasti määriteltyjen operaatioiden + ja  ^.  (jätetään merkitsemättä) suhteen:

missä a,b R.

Todistus. Todistetaan väite tarkistamalla renkaan postulaatit (R1)-(R5). Kuten edellä todettiin on (R/I, +) ryhmä. Koska (R, +) on Abelin ryhmä on myös (R/I, +) kommutatiivinen.

Osoitetaan toiseksi, että jäännösluokkien kertolasku on hyvinmääritelty. Olkoon a + I = a' + I ja b + I = b' + I, silloin a = a' + i₁ ja b = b' + i₂, joillekin i₁,i₂ I. Nyt

Koska I on renkaan R ihanne se sisältää tulot a'i₂, i₁b' ja i₁i₂ sekä näiden summan. Täten ab = a'b' + i, missä i I. Tämä tarkoittaa samaa kuin ab a'b' + I eli ab + I = a'b' + I.

Olkoon a, b, c R. Renkaan alkioiden assosiatiivisuuden nojalla saadaan postulaatin (R3) toteutuvuus:

Renkaan (R/I, +, ^. ) ykkäsalkio on 1 _R + I, missä 1_R on renkaan (R, +, ^. ) ykkösalkio. Nimittäin kaikilla a R on

Määritelmä. Rengasta (R/I, +, ^. ) sanotaan renkaan (R, +, ^. ) jäännösluokkarenkaaksi ihanteen I suhteen (voidaan sanoa myös tekijärenkaaksi (englanniksi residue class ring, factor ring)).

Linkit:
Tekijäryhmä
Rengas
Ihanne