Esimerkkejä nollanjakajista ja kokonaisalueista

Esimerkki. Renkaassa (₁₀, +, ^. ) jäännösluokat ja ovat nollanjakajia, sillä  ^.  = = .

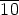Esimerkki. Matriisi on nollanjakaja renkaassa (M_n(), +, ^. ), missä operaatiot ovat matriisien yhteenlasku ja matriisitulo, sillä

Esimerkki. Osoitetaan, että renkaan (_m, +, ^. ) alkio 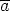on nollanjakaja jos ja vain jos ja syt(a,m) > 1.

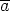
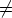
Oletetaan ensin, että ja syt(a,m) > 1. Merkitään syt(a,m) = d, silloin a = a₁d ja m = m₁d joillekin luvuille a₁ ja m₁. Nyt am₁ = a₁dm₁ = a₁m, siis = renkassa _m. Koska d > 1, niin m > m₁ ja m m₁, jot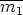en . Täten 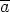on nollanjakaja.

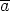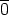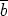
Oletetaan toiseksi, että alkio on renkaan _m nollanjakaja. Silloin on olemassa sellainen _m, , että  ^.  = . Renkaassa _m tämä tarkoittaa sitä, että m | ab. Koska ja 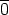, niin m a ja m b. Välttämättä siis syt(a,m) > 1 (ajattele lukujen alkutekijähajotelmaa).

Esimerkki. Edellisen esimerkin nojalla rengas (_m, +, ^. ) on kokonaisalue jos ja vain jos m on alkuluku. Silloin tämän jäännösluokkarenkaan karakteristika on m.

Esimerkki. Kaikki lukurenkaat ovat kokonaisalueita. Kaikkien sivulla Esimerkkejä renkaista esitettyjen lukurenkaiden karakteristika on 0.

Esimerkki. Olkoon p alkuluku. Binomikertoimet

kaikilla k = 1, 2,...,p - 1, ovat jaollisia luvulla p, koska p on tekijänä osoittajassa, mutta nimittäjässä se ei ole (p on alkuluku). Toisaalta tiedetään, että binomikerroin on aina kokonaisluku, joten p on binomikertoimen 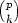tekijä, kun 0 < k < p.

Olkoon (D, +, ^. ) kokonaisalue, jonka karakteristika on p. Kokonaisalueen kommutatiivisuuden nojalla voidaan binomikaavaa käyttää laskettaessa kokonaisalueessa D sen alkioiden summan potenssia. Siis, jos a,b D, niin

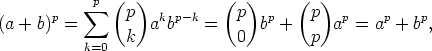
koska char (D) = p.

Linkit:
Kokonaisalue
Aritmetiikan peruslause
Esimerkkejä renkaista