Aritmetiikan peruslause

Yhdistetty luku n voidaan aina hajottaa muotoon

Jatkamalla tässä tekijöiden n₁ ja n₂ hajottamista (jos mahdollista) saadaan lopuksi luvulle n alkutekijähajotelma:

Alkutekijähajotelma voidaan kirjoittaa myös muodossa

Tätä muotoa sanotaan luvun kanoniseksi (alkutekijä)hajotelmaksi.

Esimerkki. 300 = 2 ^. 2 ^. 3 ^. 5 ^. 5 ^. 5 = 2^2 . 3 ^. 5³.

Lause. Olkoot a ja b suhteellisia alkulukuja, toisin sanoen syt(a,b) = 1. Jos a | bc, niin a | c.

Todistus. Tiedämme, että lukujen a ja b suurin yhteinen tekijä voidaan esittää muodossa 1 = ua + vb, joillakin kokonaisluvuilla u ja v. Nyt c = c ^. 1 = c(ua + vb) = uac + vbc. Koska a | uac ja oletuksen nojalla a | bc, niin a | (uac + vbc) eli a | c.

Lause. Olkoon p alkuluku. Jos p | a₁a_k (a_i ), niin p jakaa jonkin luvuista a_i.

Todistus. Jos p | a₁, niin väite on todistettu. Oletetaan, että p a₁, silloin p ja a₁ ovat suhteellisia alkulukuja. Koska p | a₁(a₂a_k) niin edellisen lauseen nojalla p | a₂a_k. Toistamalla argumenttia ensin lukuun a₂ ja sen jälkeen niin pitkälle kuin on tarve löydetään lopulta luku a_i, jonka p jakaa.

Kahden edellisen lauseen avulla voidaan todistaa seuraava aritmetiikan peruslause.

Lause. Jokainen kokonaisluku n > 1 voidaan esittää alkulukujen tulona eli muodossa

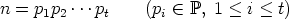
tekijöiden p_i järjestystä vaille yksikäsitteisesti.

Todistus. Alkutekijähajotelman olemassaolo perusteltiin sivun alussa. Todistetaan vielä, että kyseinen hajotelma on yksikäsitteinen. Tehdään vastaoletus, että luvulle n olisi kaksi esitystä n = p₁ p₂ p_t ja n = q₁q₂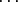q_r, missä kaikki luvut p_i ja q_i ovat alkulukuja. Silloin p₁ | q₁q₂q_r, joten edellisen lauseen nojalla p₁ jakaa jonkin luvuista q_i. Voidaan olettaa, että p₁ | q₁. Koska molemmat luvut ovat alkulukuja on p₁ = q₁. Tämän jälkeen jää tarkasteltavaksi yhtälö

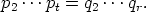
Jatkamalla samoin saadaan p₂ = q₂,...,p_t = q_r (ja r = t).

On luonnollista sopia, että luvulla 1 on esitys "tyhjänä" alkulukutulona (siis t = 0). Negatiivisilla kokonaisluvuilla on yksikäsitteinen esitys muodossa -p₁p₂p_t.

Kahden luvun a ja b suurin yhteinen tekijä voidaan laskea määrittämällä ensin lukujen kanoniset hajotelmat. Jos a ja b ovat suuria on Eukleideen algoritmi kuitenkin nopeampi menetelmä.

Linkit:
Jaollisuus ja alkuluvut
Jakoalgoritmi
Suurin yhteinen tekijä
Eukleideen algoritmi