| Sanna Ranto, LUKUTEORIA JA ALGEBRA Versio 1, 1.11.2003 | KUNTA |
Kokonaisalueen osamääräkunnan konstruktio
Olkoon (R, +, . ) rengas. Voidaanko (R, +, . ) jotenkin laajentaa kunnaksi? Laajennus on
selvästi mahdoton, jos rengas R ei ole kommutatiivinen tai joukossa R on nollanjakajia. Jos
(R, +, . ) on kokonaisalue, voidaan R laajentaa kunnaksi konstruoimalla niin sanottu
kokonaisalueen R osamääräkunta Q(R), jossa R on alirenkaana. Konstruktiossa liitetään
joukkoon R sen nollasta eroavien alkioiden b käänteisalkiot  ja lisäksi tulot a .
ja lisäksi tulot a .  =
= 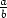 kaikilla
a
kaikilla
a  R.
R.
Esitetään konstruktio vielä yksityiskohtaisesti. Se, että konstruktio tuottaa kunnan, todistetaan sivulla Kokonaisalueen osamääräkunta.
Olkoon (D, +, . ) kokonaisalue. Muodostetaan joukko

ja määritellään tässä joukossa relaatio ~ seuraavasti:

Relaatio ~ todetaan ekvivalenssirelaatioksi tarkistamalla ekvivalenssirelaation ehdot E1-E3.
Oletetaan, että (a,b), (c,d), (e,f)  X. Selvästi ~ on refleksiivinen: (a,b) ~ (a,b). Relaation ~
symmetrisyys seuraa siitä, että kokonaisalue D on kommutatiivinen. Lisäksi ~ on transitiivinen,
sillä jos (a,b) ~ (c,d) ja (c,d) ~ (e,f), niin ad = bc ja cf = de. Koska b
X. Selvästi ~ on refleksiivinen: (a,b) ~ (a,b). Relaation ~
symmetrisyys seuraa siitä, että kokonaisalue D on kommutatiivinen. Lisäksi ~ on transitiivinen,
sillä jos (a,b) ~ (c,d) ja (c,d) ~ (e,f), niin ad = bc ja cf = de. Koska b 0, saadaan c =
0, saadaan c =  .
Sijoittamalla tämä jälkimmäiseen yhtälöön ja laventamalla alkiolla b ja supistamalla alkiolla d
saadaan af = be eli (a,b) ~ (e,f).
.
Sijoittamalla tämä jälkimmäiseen yhtälöön ja laventamalla alkiolla b ja supistamalla alkiolla d
saadaan af = be eli (a,b) ~ (e,f).
Joukko X voidaan partitioida ekvivalenssiluokkiin [(a,b)]. Näitä luokkia sanotaan formaalisiksi
osamääriksi ja niistä käytetään merkintää  . Siis
. Siis

Erityisesti 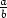 =
=  jos ja vain jos ad = bc. Kaikkien formaalisten osamäärien joukosta käytetään
merkintää Q(D). Siis
jos ja vain jos ad = bc. Kaikkien formaalisten osamäärien joukosta käytetään
merkintää Q(D). Siis

Määritellään joukossa Q(D) yhteen- ja kertolasku. Jos  ,
,
 Q(D), niin
Q(D), niin

Pitää osoittaa, että operaatiot ovat hyvinmääriteltyjä, toisin sanoen operaatioiden tulos pysyy
joukossa Q(D) ja operaatiot ovat riippumattomia ekvivalenssiluokan edustajan valinnasta.
Ensinnäkin, koska b 0D, d
0D, d 0D ja D on kokonaisalue, niin bd
0D ja D on kokonaisalue, niin bd 0D. Oletetaan sitten, että
0D. Oletetaan sitten, että
 =
= 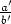 ja
ja  =
=  . Silloin ab' = ba' ja cd' = dc'. Käyttäen kokonaisalueen kommutatiivisuutta ja
distributiivilakia saadaan
. Silloin ab' = ba' ja cd' = dc'. Käyttäen kokonaisalueen kommutatiivisuutta ja
distributiivilakia saadaan

Kertolasku voidaan käsitellä samoin.
Linkit:
Kokonaisalue
Kokonaisalueen osamääräkunta
Alirengas
Ekvivalenssirelaatio
Ekvivalenssiluokka