| Sanna Ranto, LUKUTEORIA JA ALGEBRA Versio 1, 1.11.2003 | KUNTA |
Kokonaisalueen osamääräkunta
Todistetaan nyt, että sivulla Kokonaisalueen osamääräkunnan konstruktio kostruoitu systeemi todella on kunta. Yhteen- ja kertolasku määritellään kuten kyseisellä sivulla.
Lause. Kolmikko (Q(D), +, . ) on kunta. Lisäksi joukon Q(D) osajoukko

muodostaa kunnan (Q(D), +, . ) alirenkaan. Alirengas (D', +, . ) on kokonaisalue ja isomorfinen kokonaisalueen (D, +, . ) kanssa.
Todistus. Kolmikko (Q(D), +, . ) on kommutatiivinen rengas, jonka nolla-alkio on  ja
ykkösalkio
ja
ykkösalkio 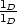 . Alkion
. Alkion 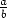
 Q(D) vasta-alkio on
Q(D) vasta-alkio on  . Rengaspostulaattien läpikäyminen jätetään
harjoitukseksi.
. Rengaspostulaattien läpikäyminen jätetään
harjoitukseksi.
Olkoon 
 Q(D). Jos
Q(D). Jos 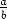

 , niin a1D
, niin a1D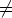 b0D eli a
b0D eli a 0D. Täten
0D. Täten 
 Q(D) ja
Q(D) ja  on
alkion
on
alkion  käänteisalkio, sillä
käänteisalkio, sillä  .
. 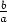 =
=  =
=  . Näin ollen rengas (Q(D), +, . ) on
kunta.
. Näin ollen rengas (Q(D), +, . ) on
kunta.
Muodostetaan kuvaus

Kuvaus j on rengashomomorfismi kuten helposti nähdään tarkistamalla ehdot RH1-RH3.
Lisäksi kuvaus j on injektio, sillä jos j(a) = j(b) eli  =
=  , niin a1D = b1D eli a = b.
Renkaiden homomorfialauseen mukaan saadaan
, niin a1D = b1D eli a = b.
Renkaiden homomorfialauseen mukaan saadaan

Sivun Rengashomomorfismin ydin ja kuva huomion perusteella (D', +, . ) on kunnan
(Q(D), +, . ) alirengas. ![[]](images/msam10-c-3.gif)
Määritelmä. Kuntaa (Q(D), +, . ) sanotaan kokonaisalueen (D, +, . ) osamääräkunnaksi tai jakokunnaksi (quotient field, field of fractions).
Jos konstruoidaan osamääräkunta (Q(D), +, . ) kokonaisalueelle (D, +, . ), joka on jonkin kunnan (K, +, . ) alirengas, niin Q(D) on isomorfinen sivun Huomioita alikunnasta lauseessa määritellyn kunnan

kanssa. On luonnollista samaistaa Q(D) ja KD, ja nimittää myös kuntaa KD kokonaisalueen D
osamääräkunnaksi. Edellisessä lauseessa todistettiin, että D on aina kunnan Q(D)
alirengas, joten osamääräkunta voidaan aina ajatella muodossa KD. Nähdään myös, että
kokonaisalueen D osamääräkunta (KD, +, . ) on suppein kunta, jonka alirengas
(D, +, . ) on. Jos nimittäin (K, +, . ) on jokin kunta ja (D, +, . ) se alirengas, niin
D  KD
KD  K.
K.
Voidaan todistaa, että kokonaisalueen osamääräkunnalla on seuraava universaalisuusominaisuus: Jos kokonaisalue A on isomorfinen kokonaisalueen B kanssa, niin kokonaisalueeen A osamääräkunta KA on isomorfinen kokonaisalueen B osamääräkunnan KB kanssa.
Linkit:
Kokonaisalueen osamääräkunnan konstruktio
Renkaiden homomorfia
Renkaiden homomorfialause
Rengashomomorfismin ydin ja kuva
Huomioita alikunnasta