Huomioita alikunnasta

Millaisia alikuntia kunnalla (K, +, ^. ) voi olla? Jokainen alikunta sisältää kunnan K ykkösalkion 1_K. Täten alikunnat sisältävät myös kaikki ykkösalkion monikerrat n1_K, missä n . Tämä johtaa seuraavaan havaintoon.

Lemma. Jokaisella kunnalla (K, +, ^. ) on alirenkaana kokonaisalue (D, +, ^. ), missä

Todistus. Muodostetaan kuvaus

Osoitetaan ensin, että kuvaus f on rengashomomorfismi. Kaikilla a,b on sivun Renkaiden aritmetiikkaa huomioiden perusteella f(a + b) = (a + b)1_K = a1_K + b1_K = f(a) + f(b). Lisäksi f(a ^. b) = (a ^. b)1 _K = a ^. b1 _K = a1_K ^. b1 _K = f(a) ^. f(b). Sivun Rengashomomorfismin ydin ja kuva perusteella (Im (f), +, ^. ) on kunnan (K, +, ^. ) alirengas (ja silloin välttämättä myös kokonaisalue).

Renkaiden homomorfialauseen perusteella / ker(f) Im (f) K. Tässä Im (f) = {n1_K | n } ja

Nyt siis D = Im (f) / ker(f), ja lemman isomorfiat seuraavat, kun huomataan, että /p = _p ja /{0} = . Sivun Esimerkkejä nollanjakajista ja kokonaisalueista mukaan (_p, +, ^. ) ja (, +, ^. ) ovat kokonaisalueita.

Lause. Olkoon kokonaisalue (D, +, ^. ) kunnan (K, +, ^. ) alirengas. Määritellään joukko

Kolmikko (K_D, +, ^. ) on kunnan (K, +, ^. ) alikunta. Lisäksi (K _D, +, ^. ) on kaikkien kunnan K alikuntien (F, +, ^. ), joilla D F, alikunta.

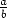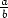Todistus. Todistetaan ensimmäinen väite käyttäen alikuntakriteeriä. Koska D K_D ja (D, +,  ^.   ) on rengas, niin {1 _D, 0_D} K_D. Olkoot , K_D. Silloin - = K_D, koska ad - bc, bd D. Jos 0_D, toisin sanoen c0_D, niin / 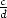= K_D.

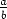Lauseen jälkimmäinen väite on ilmeinen, koska jokainen kunta (F, +, ^. ), jolle D F, sisältää alkioiden a, b D mukana osamäärän , kun b0_D.

Jos (K, +,  ^.   ) on lukukunta, sen alirengas on kokonaisalue (, +, ^. ) (lemman mukaan), ja edellisessä lauseessa esiintyvä joukko K = .

Linkit:
Alikunta
Renkaan aritmetiikkaa
Rengashomomorfismin ydin ja kuva
Renkaiden homomorfialause
Esimerkkejä nollanjakajista ja kokonaisalueista