Polynomin aste

Olkoon (R, +, ^. ) rengas ja (R[x], +, ^. ) polynomirengas yli renkaan R.

Määritelmä. Jos polynomissa f(x) = a₀ + a₁x + a₂x² + + a _nxⁿ on a _n0, kerrointa a_n sanotaan polynomin f(x) johtavaksi kertoimeksi ja lukua n sanotaan polynomin f(x) asteeksi (degree). Polynomin asteesta käytetään merkintää deg f(x).

Polynomia f(x) sanotaan pääpolynomiksi (monic polynomial), jos sen johtava kerroin on renkaan R ykkösalkio.

Yllä on määritelty polynomin johtava kerroin ja aste kaikille nollapolynomista 0_R eroaville polynomeille f(x) [x]. Nollapolynomin asteeksi sovitaan deg(0_R) = -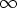. Tässä - 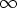ajatellaan lukuna, joka on pienempi kuin kaikki reaaliluvut.

Lause. Olkoon (R, +, ^. ) kokonaisalue. Silloin (R[x], +, ^. ) on kokonaisalue ja kaikilla f(x),g(x) R[x] on

Lisäksi

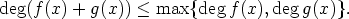
Todistus. Sivun Polynomirengas lauseen mukaan (R[x], +, ^. ) on kommutatiivinen. Olkoot f(x),g(x) R[x] ja olkoon polynomin f(x) johtava kerroin a_n ja polynomin g(x) johtava kerroin b_m. Koska (R, +, ^. ) on kokonaisalue, on a _nb_m0_R. Täten tulopolynomissa f(x)g(x) esiintyvä korkeinta astetta oleva termi on a_nb_mx^n+m. Tulopolynomi on siis eri kuin nollapolynomi, joten (R[x], +, ^. ) on kokonaisalue ja lisäksi tulopolynomin aste toteuttaa väitteen yhtälön.

Jos ainakin toinen polynomeista f(x) ja g(x) on nollapolynomi, on myös tulopolynomi f(x)g(x) = 0_R ja silloin yhtälö deg(f(x)g(x)) = deg f(x) + deg g(x) pitää paikkansa, sillä molemmat puolet ovat -.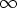

Jätetään lauseen loppuosa harjoitukseksi.

Linkit:
Polynomirengas
Esimerkkejä polynomirenkaista
Kokonaisalue