![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät
Sisällön pääryhmät  Integraali
Integraali  Hitausmomentti [ 1 2
]
Hitausmomentti [ 1 2
]
ESITIEDOT:
![[#]](kuvat/msam10-c-4.gif) määrätty integraali
määrätty integraali
KATSO MYÖS:
![[#]](kuvat/msam10-c-4.gif) integroimistekniikkaa,
integroimistekniikkaa, ![[#]](kuvat/msam10-c-4.gif) massakeskipiste
massakeskipiste
![[#]](kuvat/msam10-c-4.gif) Kansisivu Kansisivu
![[#]](kuvat/msam10-c-4.gif) Sisältö Sisältö
![[#]](kuvat/msam10-c-4.gif) Hakemisto Hakemisto |
![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät Sisällön pääryhmät  Integraali Integraali  Hitausmomentti [ 1 2
] Hitausmomentti [ 1 2
]
ESITIEDOT: ![[#]](kuvat/msam10-c-4.gif) määrätty integraali määrätty integraali
KATSO MYÖS: ![[#]](kuvat/msam10-c-4.gif) integroimistekniikkaa, integroimistekniikkaa, ![[#]](kuvat/msam10-c-4.gif) massakeskipiste massakeskipiste
|
|
Massapisteen — massana m — fysikaalinen hitausmomentti kiertoakselin suhteen on J = mr2, missä r on kohtisuora etäisyys akselista.
Jos kyseessä on kappale, saadaan sen hitausmomentti lasketuksi käyttämällä samaa ideaa kuin massakeskipisteen laskemisessa:
Kappale jaetaan pieniin osiin, esimerkiksi pikku kuutioihin koordinaattitasojen suuntaisilla tasoilla. Muunkinlaista jakoa ’pistemäisiin’ osiin voidaan käyttää. Jokaista osaa kohdellaan omana massapisteenään ja lasketaan näiden hitausmomentit yhteen:
 r
r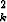
 mk,
mk,
missä  mk on k:nnen pikku kuution massa ja rk sen etäisyys kiertoakselista.
mk on k:nnen pikku kuution massa ja rk sen etäisyys kiertoakselista.
Tämä on Riemannin summa, joka kuutioita pienennettäessä lähestyy määrättyä integraalia. Yleensä kyseessä on kolmiulotteisen avaruuden integraali, mutta erikoistapauksissa se on palautettavissa yhden muuttujan integraaliksi, kuten edempänä esimerkissä osoitetaan. Integraalia kutsutaan kappaleen (fysikaaliseksi) hitausmomentiksi.
Jos kappale on homogeeninen, ts. sen massatiheys 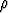 on vakio, on
on vakio, on  mk =
mk = 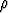
 vk,
missä
vk,
missä  vk on pikku kuution tilavuus. Tällöin
vk on pikku kuution tilavuus. Tällöin 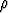 voidaan ottaa eo. summassa
tekijäksi. Jäljelle jäävä summa
voidaan ottaa eo. summassa
tekijäksi. Jäljelle jäävä summa
 r
r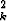
 vk
vk
riippuu vain kappaleen geometriasta ja valitusta akselisuorasta. Vastaava
integraali on kappaleen matemaattinen hitausmomentti eli toinen momentti
akselisuoran suhteen. Matemaattinen hitausmomentti saadaan siis fysikaalisesta
asettamalla massatiheydeksi vakio 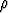 = 1.
= 1.
![[#]](kuvat/msam10-c-4.gif) massakeskipiste massakeskipiste![[#]](kuvat/msam10-c-4.gif) Riemannin summa Riemannin summa![[#]](kuvat/msam10-c-4.gif) määrätty integraali määrätty integraali |
Kivelä,  niinkuin matematiikka, versio 1.12
niinkuin matematiikka, versio 1.12