![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät
Sisällön pääryhmät  Integraali
Integraali  Integroimistekniikkaa [ 1 2 3
4 5 ]
Integroimistekniikkaa [ 1 2 3
4 5 ]
ESITIEDOT:
![[#]](kuvat/msam10-c-4.gif) integraalifunktio,
integraalifunktio, ![[#]](kuvat/msam10-c-4.gif) määrätty integraali,
määrätty integraali, ![[#]](kuvat/msam10-c-4.gif) derivointisäännöt
derivointisäännöt
KATSO MYÖS:
![[#]](kuvat/msam10-c-4.gif) Kansisivu Kansisivu
![[#]](kuvat/msam10-c-4.gif) Sisältö Sisältö
![[#]](kuvat/msam10-c-4.gif) Hakemisto Hakemisto |
![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät Sisällön pääryhmät  Integraali Integraali  Integroimistekniikkaa [ 1 2 3
4 5 ] Integroimistekniikkaa [ 1 2 3
4 5 ]
ESITIEDOT: ![[#]](kuvat/msam10-c-4.gif) integraalifunktio, integraalifunktio, ![[#]](kuvat/msam10-c-4.gif) määrätty integraali, määrätty integraali, ![[#]](kuvat/msam10-c-4.gif) derivointisäännöt derivointisäännöt
KATSO MYÖS: |
|
Annetun funktion integraalifunktiota laskettaessa funktiota pyritään muuntamaan siten, että tulos voidaan tunnistaa jonkin alkeisfunktion derivaataksi. Usein muuntaminen joudutaan tekemään useassa vaiheessa.
Tärkein menettely on sopivan sijoituksen tekeminen integraaliin. Kyseessä voi olla integraalifunktion etsiminen, jolloin integroimismuuttuja vaihdetaan toiseksi, tai määrätyn integraalin laskeminen, jolloin lisäksi muunnetaan rajat. Menettely pohjautuu yhdistetyn funktion derivoimissääntöön. Sijoitusmenettely on seuraava:
Olkoon laskettavana integraali 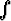 f(x) dx tai
f(x) dx tai 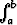 f(x) dx.
f(x) dx.
Valitaan uusi muuttuja t, jota sitoo vanhaan muuttujaan x yhtälö x = g(t). Tässä funktio g valitaan päämääränä saada integraali yksinkertaistumaan. Derivoimalla saadaan
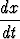 = g'(t) eli dx = g'(t) dt,
= g'(t) eli dx = g'(t) dt,
missä derivaattasymbolia 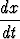 on käsitelty ikäänkuin se olisi osamäärä. Jos
kyseessä on määrätty integraali, ratkaistaan lisäksi muuttujalle t rajat
on käsitelty ikäänkuin se olisi osamäärä. Jos
kyseessä on määrätty integraali, ratkaistaan lisäksi muuttujalle t rajat  ja
ja 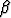 yhtälöistä a = g(
yhtälöistä a = g( ) ja b = g(
) ja b = g(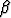 ).
).
Sijoitetaan tulokset integraaliin:
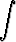 f(x) dx =
f(x) dx = 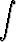 f(g(t))g'(t) dt tai
f(g(t))g'(t) dt tai 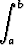 f(x) dx =
f(x) dx = 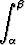 f(g(t))g'(t) dt.
f(g(t))g'(t) dt.
Sijoitus voidaan aivan yhtä hyvin tehdä uuden muuttujan t suhteen ratkaistuista
muodoista, mikäli tämä on helpompaa: t = h(x), dt = h'(x) dx,  = h(a),
= h(a),
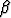 = h(b).
= h(b).
![[#]](kuvat/msam10-c-4.gif) integraalifunktio integraalifunktio![[#]](kuvat/msam10-c-4.gif) derivointi (alkeisfunktioiden) derivointi (alkeisfunktioiden)![[#]](kuvat/msam10-c-4.gif) määrätty integraali määrätty integraali![[#]](kuvat/msam10-c-4.gif) derivaatta (yhdistetyn funktion) derivaatta (yhdistetyn funktion)![[#]](kuvat/msam10-c-4.gif) yhtälö yhtälö |
Kivelä,  niinkuin matematiikka, versio 1.12
niinkuin matematiikka, versio 1.12