![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät
Sisällön pääryhmät  Integraali
Integraali  Integroimistekniikkaa [ 1 2 3
4 5 ]
Integroimistekniikkaa [ 1 2 3
4 5 ]
ESITIEDOT:
![[#]](kuvat/msam10-c-4.gif) integraalifunktio,
integraalifunktio, ![[#]](kuvat/msam10-c-4.gif) määrätty integraali,
määrätty integraali, ![[#]](kuvat/msam10-c-4.gif) derivointisäännöt
derivointisäännöt
KATSO MYÖS:
![[#]](kuvat/msam10-c-4.gif) Kansisivu Kansisivu
![[#]](kuvat/msam10-c-4.gif) Sisältö Sisältö
![[#]](kuvat/msam10-c-4.gif) Hakemisto Hakemisto |
![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät Sisällön pääryhmät  Integraali Integraali  Integroimistekniikkaa [ 1 2 3
4 5 ] Integroimistekniikkaa [ 1 2 3
4 5 ]
ESITIEDOT: ![[#]](kuvat/msam10-c-4.gif) integraalifunktio, integraalifunktio, ![[#]](kuvat/msam10-c-4.gif) määrätty integraali, määrätty integraali, ![[#]](kuvat/msam10-c-4.gif) derivointisäännöt derivointisäännöt
KATSO MYÖS: |
|
3) Hieman hankalampana esimerkkinä olkoon seuraava, missä integraali aluksi jaetaan kahteen osaan:
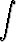
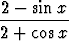 dx =
dx = 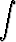
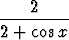 dx +
dx + 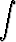
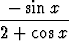 dx.
dx.
Tässä jälkimmäiseen sijoitetaan t = 2 + cos x, jolloin dt = - sin x dx. Syynä on se, että osoittaja on sama kuin nimittäjän derivaatta ja osoittajassa on siis suoraan dt. Edelliseen integraaliin sijoitetaan hieman erikoisempaa: u = tan(x/2) eli x = 2 arctan u, jolloin
dx = 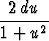 .
.
Trigonometrian kaavojen avulla voidaan osoittaa, että
cos x =  =
= 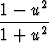 .
.
Integraali muuntuu siis muotoon
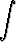
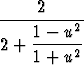
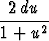 +
+ 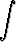
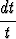 =
= 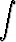
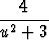 du +
du + 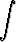
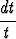 .
.
Jälkimmäinen integroituu suoraan logaritmiksi. Edellinen voidaan sijoituksella
u = 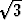 v, du =
v, du = 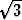 dv palauttaa arctan-funktioon:
dv palauttaa arctan-funktioon:
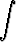
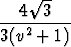 dv +
dv + 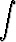
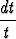 =
= 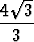 arctan v + ln t + C.
arctan v + ln t + C.
Palaamalla alkuperäiseen muuttujaan x saadaan
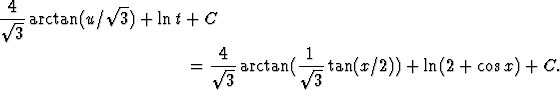
![[#]](kuvat/msam10-c-4.gif) integraalifunktio integraalifunktio![[#]](kuvat/msam10-c-4.gif) trigonometria (johdannaiskaavat) trigonometria (johdannaiskaavat)![[#]](kuvat/msam10-c-4.gif) arcus-funktio arcus-funktio![[#]](kuvat/msam10-c-4.gif) integrointi (kaavat) integrointi (kaavat)![[#]](kuvat/msam10-c-4.gif) integrointi (kaavat) integrointi (kaavat) |
Kivelä,  niinkuin matematiikka, versio 1.12
niinkuin matematiikka, versio 1.12