![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät
Sisällön pääryhmät  Integraali
Integraali  Hitausmomentti [ 1 2
]
Hitausmomentti [ 1 2
]
ESITIEDOT:
![[#]](kuvat/msam10-c-4.gif) määrätty integraali
määrätty integraali
KATSO MYÖS:
![[#]](kuvat/msam10-c-4.gif) integroimistekniikkaa,
integroimistekniikkaa, ![[#]](kuvat/msam10-c-4.gif) massakeskipiste
massakeskipiste
![[#]](kuvat/msam10-c-4.gif) Kansisivu Kansisivu
![[#]](kuvat/msam10-c-4.gif) Sisältö Sisältö
![[#]](kuvat/msam10-c-4.gif) Hakemisto Hakemisto |
![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät Sisällön pääryhmät  Integraali Integraali  Hitausmomentti [ 1 2
] Hitausmomentti [ 1 2
]
ESITIEDOT: ![[#]](kuvat/msam10-c-4.gif) määrätty integraali määrätty integraali
KATSO MYÖS: ![[#]](kuvat/msam10-c-4.gif) integroimistekniikkaa, integroimistekniikkaa, ![[#]](kuvat/msam10-c-4.gif) massakeskipiste massakeskipiste
|
|
Lasketaan R-säteisen pallon hitausmomentti keskipisteen kautta kulkevan akselin
suhteen, kun massatiheys on vakio 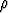 = 1.
= 1.
Sijaitkoon kolmiulotteinen xyz-koordinaatisto siten, että origo on pallon
keskipisteessä. Kiertoakseli olkoon z-akseli. Pallo jaetaan edellä kuvatulla tavalla
pikku osiin ja näistä kerätään yhteen ne, joilla on sama etäisyys kiertoakselista.
Yhteen kuuluvat osat muodostavat lieriökuoria akselina z-akseli. Jos etäisyys
akselista on r, on lieriön korkeus Pythagoraan mukaan 2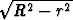 ja pohjan säde
luonnollisesti r. Jos lieriökuoren paksuus on
ja pohjan säde
luonnollisesti r. Jos lieriökuoren paksuus on  r, on kuoren tilavuus (eli massa,
koska
r, on kuoren tilavuus (eli massa,
koska 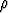 = 1) likimain 2
= 1) likimain 2 r 2
r 2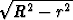
 r.
r.
Jakamalla pallo n lieriökuoreen, muodostamalla jokaisen hitausmomentti ja laskemalla yhteen saadaan Riemannin summa, joka approksimoi pallon hitausmomenttia:
 r
r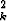 . 2
. 2 rk 2
rk 2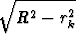
 rk.
rk.
Jakoa tihennettäessä, so. kuoria ohennettaessa, jolloin niiden lukumäärä kasvaa, tämä lähestyy integraalia
J = 4
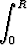 r3
r3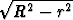 dr,
dr,
mikä siis antaa pallon hitausmomentin.
Integraali voidaan laskea tekemällä sijoitus t = 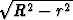 , jolloin dt = -
, jolloin dt = -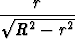 dr
ja uudet rajat ovat t = R, t = 0. Integraali saa seuraavan muodon ja voidaan
laskea:
dr
ja uudet rajat ovat t = R, t = 0. Integraali saa seuraavan muodon ja voidaan
laskea:
J = 4
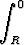 - (R2 - t2)t2 dt = -4
- (R2 - t2)t2 dt = -4
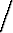
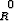
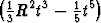 =
= 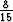
 R5.
R5.
Hitausmomentti lausutaan yleensä kappaleen kokonaismassan avulla. Koska
massatiheys = 1, on kokonaismassa sama kuin tilavuus: m = 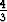
 R3. Tällöin pallon
hitausmomentti voidaan kirjoittaa
R3. Tällöin pallon
hitausmomentti voidaan kirjoittaa
J =  mR2.
mR2.
Tämä vastaa tilannetta, jossa pallon massa on keskittynyt yhteen pisteeseen
etäisyydelle 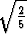 R. Tätä etäisyyttä sanotaan pallon hitaussäteeksi.
R. Tätä etäisyyttä sanotaan pallon hitaussäteeksi.
![[#]](kuvat/msam10-c-4.gif) pallo pallo![[#]](kuvat/msam10-c-4.gif) koordinaatisto (xyz-) koordinaatisto (xyz-)![[#]](kuvat/msam10-c-4.gif) lieriö lieriö![[#]](kuvat/msam10-c-4.gif) Pythagoraan lause Pythagoraan lause![[#]](kuvat/msam10-c-4.gif) pohja (lieriön) pohja (lieriön)![[#]](kuvat/msam10-c-4.gif) Riemannin
summa Riemannin
summa![[#]](kuvat/msam10-c-4.gif) määrätty integraali määrätty integraali![[#]](kuvat/msam10-c-4.gif) integrointi (sijoitus) integrointi (sijoitus)![[#]](kuvat/msam10-c-4.gif) pallo (tilavuus) pallo (tilavuus) |
Kivelä,  niinkuin matematiikka, versio 1.12
niinkuin matematiikka, versio 1.12