![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät
Sisällön pääryhmät  Diskreettiä matematiikkaa
Diskreettiä matematiikkaa  Matemaattinen
induktio [ 1 2 ]
Matemaattinen
induktio [ 1 2 ]
ESITIEDOT:
KATSO MYÖS:
![[#]](kuvat/msam10-c-4.gif) logiikka
logiikka
![[#]](kuvat/msam10-c-4.gif) Kansisivu Kansisivu
![[#]](kuvat/msam10-c-4.gif) Sisältö Sisältö
![[#]](kuvat/msam10-c-4.gif) Hakemisto Hakemisto |
![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät Sisällön pääryhmät  Diskreettiä matematiikkaa Diskreettiä matematiikkaa  Matemaattinen
induktio [ 1 2 ] Matemaattinen
induktio [ 1 2 ]
ESITIEDOT: KATSO MYÖS: ![[#]](kuvat/msam10-c-4.gif) logiikka logiikka
|
|
Todistetaan induktiolla luonnollisten lukujen 1, 2, ..., n neliöiden summaa koskeva väittämä P (n) eli
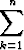 k2 =
k2 = 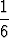 n(n + 1)(2n + 1).
n(n + 1)(2n + 1).
oikeaksi kaikilla luonnollisilla luvuilla n.
1) Arvolla n = 1 on
 k2 = k2 =  k2 = 1 ja k2 = 1 ja | ||||
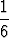 n(n + 1)(2n + 1) = n(n + 1)(2n + 1) = 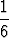 1(1 + 1)(2 . 1 + 1) = 1. 1(1 + 1)(2 . 1 + 1) = 1. |
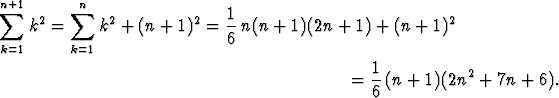
Toisen yhtäläisyysmerkin kohdalla on käytetty oletusta, että P (n) on tosi. Toisaalta väittämän P (n + 1) oikea puoli on
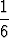 (n + 1)[(n + 1) + 1][2(n + 1) + 1] =
(n + 1)[(n + 1) + 1][2(n + 1) + 1] = 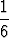 (n + 1)(2n2 + 7n + 6).
(n + 1)(2n2 + 7n + 6).
P (n + 1) on siis tosi, koska sen vasen ja oikea puoli ovat samat.
![[#]](kuvat/msam10-c-4.gif) luonnollinen
luku luonnollinen
luku![[#]](kuvat/msam10-c-4.gif) summamerkintä summamerkintä |
Kivelä,  niinkuin matematiikka, versio 1.12
niinkuin matematiikka, versio 1.12