Sisällön pääryhmät Luvut Lukujärjestelmät [ 1 2 3 ] ESITIEDOT: KATSO MYÖS:  potenssi

Kansisivu  Sisältö  Hakemisto

Lukujärjestelmän kantaluku voi olla muukin luonnollinen luku (> 1) kuin 10. Jos kantaluku on b, ovat järjestelmän numerot 0,  1,  ...,  b - 1. Esitettäessä jotakin lukua b-kantaisessa järjestelmässä, kirjoitetaan näitä numeroita peräkkäin samaan tapaan kuin kymmenjärjestelmässä kirjoitetaan numeroita 0,  1,  ...,  9. Myös desimaalipistettä voidaan käyttää, vaikka nimitys ’desimaali’ ei enää olekaan paikallaan.

Yleisesti varsinkin tietotekniikassa käytettyjä lukujärjestelmiä ovat binääri-, oktaali- ja heksadesimaalijärjestelmä; näiden kantaluvut ovat 2, 8 ja 16. Binäärijärjestelmän numerot ovat 0 ja 1; oktaalijärjestelmän 0,  1,  2,  3,  4,  5,  6,  7. Heksadesimaalijärjestelmässä numeroita tarvitaan kuusitoista, jolloin avuksi otetaan aakkosten alkupään kirjaimet: 0,  1,  2,  3,  4,  5,  6,  7,  8,  9,  A,  B,  C,  D,  E,  F.

Mitä lukua tietty esitys tarkoittaa, lasketaan samalla tavoin kuin edellä kymmenjärjestelmän tapauksessa: Jos luvut a_i tarkoittavat järjestelmän numeroita, tulkitaan seuraavasti:

a_n...a₂a₁a₀ . a_-1a_-2a_-3...a_-m = 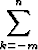a_k ^. b^k.

Kun yhtäläisyysmerkin oikea puoli lasketaan (kymmenjärjestelmässä), saadaan luvun esitys kymmenjärjestelmässä.

On siis ajateltava, että ’luku’ sinänsä on jotakin esitysjärjestelmästä riippumatonta. Se voidaan valinnan mukaan esittää eri järjestelmissä, joista kymmenjärjestelmä on ihmiselle tutuin. Tietokonetekniikalle luonnollisin on binäärijärjestelmä — tai sen johdannaisina oktaali- tai heksadesimaalijärjestelmä — koska sähköisillä ja magneettisilla ilmiöillä on kaksi tilaa vastaten binäärijärjestelmän kahta numeroa.

luonnollinen luku  summamerkintä  potenssi (kokonaisluku-)

Kivelä, niinkuin matematiikka, versio 1.12