6 Derivaatta
6.1 Derivaatta ja differentiaali
Tehtävä 172
Olkoon f(x) = x4. Etsi derivaatan määritelmän avulla f'(-3).Tehtävä 173
Muodosta funktion f(x) =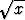 derivaatta suoraan määritelmän mukaan, so.
tarkastelemalla erotusosamäärän raja-arvoa.
derivaatta suoraan määritelmän mukaan, so.
tarkastelemalla erotusosamäärän raja-arvoa.
Tehtävä 174
Todista: Jos f on derivoituva kohdassa a ja c on vakio, niin cf on derivoituva kohdassa a ja (cf) = c
(cf) = c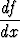 .
.
Tehtävä 175
Todista: xn = nxn-1 kaikilla x
xn = nxn-1 kaikilla x 
 , n
, n 
 .
.
Tehtävä 176
Osoita esimerkillä, että f + g voi olla kaikkialla derivoituva, vaikka funktioilla f ja g ei ole millään muuttujan arvolla derivaattaa.Tehtävä 177
Funktio f on määritelty välillä ] - 1, 1[ ja derivaatta f' on olemassa pisteessä x = 0 (mutta ei välttämättä muualla). Määritä tarkasti perustellen
limx 0
0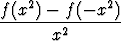 .
.
Tehtävä 178
Funktio f toteuttakoon eräässä origon ympäristössä epäyhtälön |f(x)| < x2. Todista, että f'(0) on olemassa ja määritä sen arvo.Tehtävä 179
Olkoon f(x) = x3. Määritä sup S, kun
S = 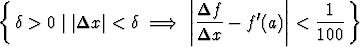
ja a) a = 0, b) a = 1, c) a = 3. Miten tehtävä liittyy derivaatan määritelmään?
Tehtävä 180
Olkoon f(0) = 0 ja f'(0) = 2. Todista, että on olemassa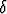 > 0 siten, että
0 < |x| <
> 0 siten, että
0 < |x| < 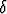
 1 < f(x)/x < 3.
1 < f(x)/x < 3.
Tehtävä 181
Oletetaan, että f'(a) on olemassa. Määritä seuraavat raja-arvot:
a) limh 0
0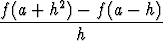 , b) limx
, b) limx a
a .
.
Tehtävä 182
Olkoon f''(a) olemassa. Määritä
limt 0
0 .
.
Tehtävä 183
Muodosta funktion f(x) = 1/x2 differentiaali ja korjaustermi pisteessä x = 2. Totea, että korjaustermin -funktiolla on vaadittu raja-arvo-ominaisuus.
-funktiolla on vaadittu raja-arvo-ominaisuus.
Tehtävä 184
Muodosta funktion f lisäys f = f(x + h) - f(x), vastaava differentiaali
df(x, h) ja korjaustermi h
f = f(x + h) - f(x), vastaava differentiaali
df(x, h) ja korjaustermi h (x, h), kun
(x, h), kun
a) f(x) = x3, b) f(x) = 3x2 - 5x + 2, c) f(x) =  , d) f(x) =
, d) f(x) =  .
.
Tarkista, onko  -funktiolla derivoituvuudessa vaadittu raja-arvo-ominaisuus.
-funktiolla derivoituvuudessa vaadittu raja-arvo-ominaisuus.
Tehtävä 185
Laske differentiaalin avulla likiarvo luvulle a) , b)
, b)  , c)
, c)  ,
d)
,
d) 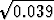 . Määritä oikaisun itseisarvolle likimääräinen yläraja. Saadaanko ylä- vai
alalikiarvo?
. Määritä oikaisun itseisarvolle likimääräinen yläraja. Saadaanko ylä- vai
alalikiarvo?
Tehtävä 186
Olkoon
f(x) =  .
.
Laske differentiaalin avulla likiarvo luvulle f(7.005). Montako oikeaa desimaalia on vastauksessa?
Tehtävä 187
Laske likiarvo luvulle valitsemalla a) x = 81 ja
valitsemalla a) x = 81 ja  x = 9, b) x = 100 ja
x = 9, b) x = 100 ja
 x = -10. Vertaa tulosta oikeaan 4-desimaaliseen likiarvoon 9.4868.
x = -10. Vertaa tulosta oikeaan 4-desimaaliseen likiarvoon 9.4868.
Tehtävä 188
Osoita differentiaalikehitelmää käyttäen, että funktio f(x) = 3 + ei ole differentioituva kohdassa x = 2.
ei ole differentioituva kohdassa x = 2.
6.2 Derivoimissääntöjä
Tehtävä 189
Derivoi seuraavat funktiot:| a) (x2 + 2x + 1)(x2 - 2x + 1), | b) (4x + 1)2(x2 - 2)3, | c) 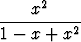 , , | |||||||||
d) 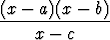 , , | e)  , , | f)  5. 5. |
Tehtävä 190
Olkoon
f(x) = 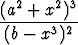 .
.
Määritä derivaatan f'(x) nollakohdat.
Tehtävä 191
Määritä f(n)(x), kun f(x) on
a) f(x) =  , b) f(x) =
, b) f(x) = 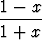 , c) f(x) =
, c) f(x) = 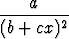 .
.
Tehtävä 192
Polynomilla p(x) = x3 + ax2 + bx + c on nollakohta, joka on myös sen derivaattojen p' ja p'' nollakohta. Osoita, että p on erään polynomin kuutio.Tehtävä 193
Osoita, että jos (x - c)2 on polynomin p(x) tekijä, niin p'(c) = 0. Etsi sellaiset luvut a, että polynomilla x3 + 8x2 - 44x + a on kaksinkertainen nollakohta.Tehtävä 194
Funktion x3 + ax2 + bx + c derivaatta häviää, kun x = -1 ja funktion kuvaaja on symmetrinen origon suhteen. Määritä a, b ja c.Tehtävä 195
Olkoot f ja g kolmesti derivoituvia ja w(x) = f(x)g(x). Laske w''(x) ja w''' (x).Tehtävä 196
Piirrä funktion y = f(x) kuvaaja, etsi käänteiskuvauksen x = g(y) lauseke ja piirrä kuvaaja seuraavien funktioiden tapauksissa; laske myös f'(x0) ja g'(y0) annetuissa pisteissä. Miten derivaattojen arvot sopivat yhteen käänteisfunktion derivaattaa koskevan lauseen kanssa?| a) f(x) = 1 - 3x, x0 = 2, y0 = -5, | b) f(x) = 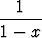 , x0 = , x0 =  , y0 = , y0 =  , , | ||||||
c) f(x) =  , x0 = -4, y0 = - , x0 = -4, y0 = -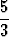 , , | d) f(x) =  , x0 = 8, y0 = 29. , x0 = 8, y0 = 29. |
Tehtävä 197
Derivoi seuraavat funktiot:a) x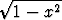 , , | b)  , , | c)  , , | d) 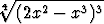 , , | ||||||||||||
e)  , , | f) 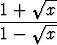 , , | g)  . . |
Tehtävä 198
Määritä funktion y = x2 - 4x - 3 käänteiskuvauksen ylemmän haaran derivaatta arvolla y = 2 a) käänteisfunktion derivoimissäännön avulla, b) määrittämällä käänteiskuvauksen lauseke.Tehtävä 199
Piirrä funktion y(x) = x4 - 2x2 - 1 kuvaaja. Millä reaaliakselin alueilla funktiolla on käänteisfunktio x(y)? Piirrä käänteisfunktioiden kuvaajat ja etsi niiden lausekkeet. Laske derivaatat y'(3) ja x'(62). Miten nämä suhtautuvat toisiinsa? Miksi?Tehtävä 200
Olkoon s = s(t) derivoituva funktio siten, että t = f(s). Lausu s'(t) muuttujan s avulla, kun a) f(s) = 3 - 2s + s3, b) f(s) = .
.
Tehtävä 201
Olkoon f'(x) = f(x) kaikilla x
 . Todista, että jos g(y) on funktion f
käänteisfunktio, niin g'(y) =
. Todista, että jos g(y) on funktion f
käänteisfunktio, niin g'(y) =  . Älä käytä hyväksi tietoa, että f itse asiassa on muotoa
f(x) = Cex , C vakio.
. Älä käytä hyväksi tietoa, että f itse asiassa on muotoa
f(x) = Cex , C vakio.
Tehtävä 202
Funktio f olkoon funktion g käänteisfunktio, jolloin f(x) = y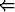
 g(y) = x.
Olkoon g kahdesti derivoituva ja g'(y)
g(y) = x.
Olkoon g kahdesti derivoituva ja g'(y)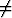 0. Osoita:
0. Osoita:
f''(x) = - .
.
Johda vastaava kaava derivaatalle f'''(x) olettaen, että g on kolmesti derivoituva.
Tehtävä 203
Olkoon y = y(x) kahdesti derivoituva funktio siten, että a) x3 + y3 = 1, b) y2 - 2xy + b2 = 0, c) x4 + y4 = x2y2, d) x4y4 = x4 + y4. Lausu y''(x) muuttujan x ja funktion y avulla.6.3 Alkeisfunktioiden derivaatat
Tehtävä 204
Johda funktion tan derivaatan lauseke lähtemällä tangentin derivaatasta.
tan derivaatan lauseke lähtemällä tangentin derivaatasta.
Tehtävä 205
Johda funktioiden arsinh x ja cosh x derivaatat käänteisfunktion
derivoimissääntöä käyttäen.
cosh x derivaatat käänteisfunktion
derivoimissääntöä käyttäen.
Tehtävä 206
Derivoi funktiot
a) e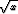 , b)
, b)  .
.
Tehtävä 207
Hermiten polynomit määritellään seuraavasti:
Hn(x) = ex2
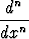 e-x2
, n = 0, 1, 2, . . . .
e-x2
, n = 0, 1, 2, . . . .
Laske H0 (x), H1(x), H2(x) ja H3(x). Osoita, että näillä on ominaisuudet
a) Hn+1 (x) + 2xHn(x) + 2nHn-1(x) = 0, b) Hn(x) = H'n-1(x) - 2xHn-1(x).
Tehtävä 208
Osoita, että funktio
y = e- sin
sin 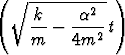
toteuttaa differentiaaliyhtälön
m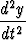 +
+ 
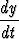 + ky = 0.
+ ky = 0.
Tehtävä 209
Derivoi seuraavat funktiot:
a) ln 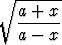 , b) ln(ln x), c) ln(x +
, b) ln(ln x), c) ln(x + 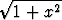 ).
).
Tehtävä 210
Olkoon z(x) = ln y(x), missä y(x) on yhtälön x = ey + y määrittelemä funktio. Laske z'(e + 1).Tehtävä 211
Olkoot f ja g kaksi kahdesti derivoituvaa funktiota, jotka toteuttavat identiteetin
af(x)g(x) + bf(x) + cg(x) + d  0,
0,
missä a, b, c ja d ovat vakioita. Olkoot lisäksi f, sen derivaatta f' ja vakiot a ja c positiivisia. Osoita, että jos vakiot täyttävät sopivan ehdon, niin
D ln  = k
= k ,
,
missä k on vakio. Mikä on ehto ja mikä on vakio k?
Tehtävä 212
Derivoi funktiota) a-1/x, b) atan x, c) logxa, d) log2(log3(ln x)).
Tehtävä 213
Derivoi funktiota) xx, b) x1/x, c) xln x, d) xxx , e) (xx)x, f) axxa.
Tehtävä 214
Piirrä käyrä xy = yx. Laske y' implisiittisellä derivoinnilla.Tehtävä 215
Derivoi seuraavat funktiot:
a) cos n , b)
, b)  , c) cot
, c) cot  , d) cos 2
, d) cos 2 .
.
Tehtävä 216
Derivoi funktio cos xesin x.Tehtävä 217
Derivoi funktiot
a) ln cos  , b) x[sin(ln x) + cos(ln x).
, b) x[sin(ln x) + cos(ln x).
Tehtävä 218
Määritä funktion
f(x) =  +
+ 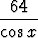
arvo sellaisissa välin ]0,  /2[ pisteissä, missä f'(x) = 0.
/2[ pisteissä, missä f'(x) = 0.
Tehtävä 219
Millä muuttujan arvoilla funktio
f(x) = 
on derivoituva?
Tehtävä 220
Lausu implisiittisen derivoinnin avulla y'(x) muuttujien x ja y funktiona, kun a) y + x = sin y cos x, b) yx = sin y + cos x.Tehtävä 221
Yhtälö y = sin(x + ay), missä a - 1, määrittelee funktion y = y(x) sen
pisteen ympäristössä, missä yhtälön kuvaaja leikkaa positiivisen x-akselin lähinnä origoa.
Määritä funktion derivaatta tässä pisteessä. Piirrä kuvaaja.
- 1, määrittelee funktion y = y(x) sen
pisteen ympäristössä, missä yhtälön kuvaaja leikkaa positiivisen x-akselin lähinnä origoa.
Määritä funktion derivaatta tässä pisteessä. Piirrä kuvaaja.
Tehtävä 222
Derivoi funktio
f(x) = 2  tan x +
tan x +  sin
sin  .
.
Millä muuttujan arvoilla derivaatta on = 0? Piirrä funktion kuvaaja.
Tehtävä 223
Derivoi funktiota)  cos cos , , | b)  sin sin  , , | c) 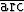 cos cos  , , | |||||||||
d)  + + 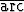 cos x, cos x, | e)  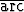 tan tan  , , | f) (x2 - 2)  sin sin 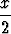 + +   . . |
Tehtävä 224
Määritellään funktio f :
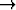
 asettamalla f(x) = x2 sin
asettamalla f(x) = x2 sin 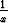 , kun x
, kun x 0, ja
f(0) = limx
0, ja
f(0) = limx 0f(x). Onko funktio jatkuva? Laske funktion derivaatta origossa. Osoita,
että derivaattafunktio f' ei ole jatkuva origossa.
0f(x). Onko funktio jatkuva? Laske funktion derivaatta origossa. Osoita,
että derivaattafunktio f' ei ole jatkuva origossa.
Tehtävä 225
Osoita, että funktio
y(x) = C1 sin x + C2 cos x + cos x ln 
toteuttaa differentiaaliyhtälön y'' + y = tan x. Luvut C1 ja C2 ovat vakioita.
Tehtävä 226
Derivoi funktiot
a) ln(cosh x), b)  tan(tanh x), c) tanh(ln x).
tan(tanh x), c) tanh(ln x).
Tehtävä 227
Derivoi funktiot
a) arsinh ex, b)  cosh
cosh  , c) 2 artanh(tan
, c) 2 artanh(tan  ), d) arcoth
), d) arcoth  .
.
6.4 Derivaatan ominaisuuksia
Tehtävä 228
Osoita derivoimalla, että funktioiden
 ja -
ja - 
erotus on vakio. Mikä on vakion arvo?
Tehtävä 229
Olkoon f derivoituva välillä I. Osoita, että derivaatan f' kahden peräkkäisen nollakohdan välissä voi olla korkeintaan yksi funktion f nollakohta.Tehtävä 230
Olkoon p polynomi, jonka nollakohdat ovat reaaliset. Todista, että derivaattapolynomin p' nollakohdat ovat myös reaaliset.Tehtävä 231
Määritä väliarvolauseessa esiintyvä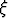 funktiolle a)
funktiolle a) 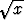 välillä [36, 49];
b) Ax2 + Bx + C välillä [a, b].
välillä [36, 49];
b) Ax2 + Bx + C välillä [a, b].
Tehtävä 232
Määritä väliarvolauseessa esiintyvä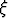 funktiolle
funktiolle
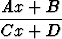 ,
,
välillä [a, b], joka ei sisällä epäjatkuvuuskohtaa x = -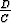 . Oletetaan AD - BC
. Oletetaan AD - BC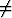 0, C
0, C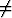 0.
0.
Tehtävä 233
Käyrän y = x4 pisteiden (-1, 1) ja (t, t4) kautta asetetaan suora. Väliarvolauseen mukaan on käyrällä piste (c, c4), jossa tangentti on mainitun suoran suuntainen. Tässä c = c(t). Määritä c(t) ja c'(t), kun a) t = 0, b) t = 1.Tehtävä 234
Funktio f olkoon jatkuva välillä [a, b] ja derivoituva arvolla x0 ]a, b[. Näytä,
että on olemassa luku M > 0 siten, että
]a, b[. Näytä,
että on olemassa luku M > 0 siten, että
x  [a, b]
[a, b]  |f(x) - f(x0)| < M|x - x0|.
|f(x) - f(x0)| < M|x - x0|.
Tehtävä 235
Olkoon f jatkuva välillä [a, b] ja derivoituva samalla välillä paitsi mahdollisesti arvolla x0 [a, b]. Todista, että jos limx
[a, b]. Todista, että jos limx x0f'(x) on olemassa ja on = A,
niin f' (x0) on olemassa ja on = A.
x0f'(x) on olemassa ja on = A,
niin f' (x0) on olemassa ja on = A.
Tehtävä 236
Olkoon f derivoituva suljetulla välillä [a, b] ja f'(a) = A sekä f'(b) = B. Todista, että jos C on lukujen A ja B välissä oleva arvo, niin on olemassa arvo c ]a, b[
siten, että f' (c) = C.
]a, b[
siten, että f' (c) = C.
Tehtävä 237
Osoita:
0 < a < b  1 -
1 - 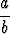 < ln
< ln  <
< 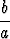 - 1.
- 1.
Tehtävä 238
Todista, että jos p > 0, niin yhtälöllä x3 + px + q = 0 on vain yksi reaalijuuri.Tehtävä 239
Olkoon f joukossa + positiivinen, aidosti kasvava ja derivoituva. Näytä,
että myös funktio g(x) = [f(1/x)]-1 on joukossa
+ positiivinen, aidosti kasvava ja derivoituva. Näytä,
että myös funktio g(x) = [f(1/x)]-1 on joukossa  + aidosti kasvava.
+ aidosti kasvava.
Tehtävä 240
Määritä
inf  .
.
Tehtävä 241
Osoita, että a) funktio 2 ln x + x2 - 4x + 1 on kasvava, b) funktio + ln x - x
on vähenevä.
+ ln x - x
on vähenevä.
Tehtävä 242
Olkoon a [0, 1[ vakio. Todista:
[0, 1[ vakio. Todista:
x  [a, 1]
[a, 1] 
 sin x <
sin x < 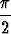 -
- 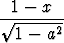 .
.
Tehtävä 243
Todista: tan x > x -
tan x > x -  x3 kaikilla x > 0.
x3 kaikilla x > 0.
Tehtävä 244
Määritä ne positiiviluvut a, joilla yhtälöllä x + a sin x - 2 = 0 on ratkaisu välillä [0, /2].
/2].
Tehtävä 245
Tutki seuraavien funktioiden ääriarvoja:| a) y = x3 - 2ax2 + a2x, | b) y = x +  , , | ||||||
c) y = x +  , , | d) y = x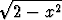 . . |
Tehtävä 246
Määritä seuraavien funktioiden ääriarvot ja piirrä kuvaajat:| a) | sin x| + cos x, | b) cos(sin x), | c)  , , | |||||||||
d)  , , | e) 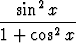 . . |
Tehtävä 247
Määritä seuraavien funktioiden ääriarvot ja piirrä kuvaajat:a) y = x1-ln x, b) y = xe1/x, c) y = (x - 1)x-1.
Tehtävä 248
Määritä funktion y = 4 tanh x + coth x ääriarvot. Piirrä kuvaaja.Tehtävä 249
Tutki funktiota f(x) = xx, x > 0. Määritä ääriarvot, piirrä kuvaaja.Tehtävä 250
Tutki, onko funktiolla f(x) = (1 - ex)7(1 - x)13 suhteellista ääriarvoa origossa. Piirrä funktion kuvaaja.Tehtävä 251
Olkoot kaikkialla jatkuvan funktion ääriarvot oleellisia. Osoita, että maksimit ja minimit esiintyvät vuorotellen.Tehtävä 252
Olkoot käyrät y = f(x) ja y = g(x) alaspäin kuperia välillä [a, b]. Todista, että käyrä y = f(x) + g(x) on alaspäin kupera mainitulla välillä.Tehtävä 253
Määritä käyrän
y = 
ääriarvopisteet ja käännepisteet. Millä muuttujan arvoilla käyrä on alaspäin, millä ylöspäin kupera? Piirrä kuvaaja.
Tehtävä 254
Tutki seuraavien käyrien kuperuutta ja määritä käännepisteet:| a) y = x + 36x2 - 2x3 - x4, | b) y = (x2 - 6x)5, | c) y =  , , | |||||||||
d) y =  , , | e) y = a - 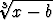 . . |
Tehtävä 255
Määritä käyrän y = sin 4x ääriarvo ja käännepisteet.Tehtävä 256
Määritä käyrien a) y = xe-x, b) y = e2x sin 2x ääriarvo- ja käännepisteet. Piirrä kuvaajat.Tehtävä 257
Määritä käyrältäy = e(x-1)2
pisteet, joiden etäisyydellä pisteestä (1, a) on ääriarvo. Määritä ääriarvojen lukumäärä ja laatu parametrin a eri arvoilla.
Tehtävä 258
Millä vakioiden a ja b arvoilla piste (1, 3) on käyrän y = ax3 + bx2 käännepiste?Tehtävä 259
Olkoon kaikkialla kahdesti derivoituva funktio f kasvava ja alaspäin kupera. Osoita, että funktio g(x) = f(x2) on alaspäin kupera.Tehtävä 260
Osoita, että käyrän y = a4x5 - 6a3x4 + 4a2x3 käännepisteet ovat samalla
suoralla. Määritä tämän suoran yksikkösuuntavektori.
a4x5 - 6a3x4 + 4a2x3 käännepisteet ovat samalla
suoralla. Määritä tämän suoran yksikkösuuntavektori.
Tehtävä 261
Millä vakion a arvoilla käyrällä
y = 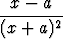
on käännepisteitä? Määritä myös ääriarvopisteet ja asymptootit ja piirrä kuvaaja.