7 Derivaatan sovellutuksia
7.1 Derivaatta tangentin kulmakertoimena
Tehtävä 262
Määritä a, b ja c siten, että käyrät y = x2 + ax + b ja y = cx - x2 sivuavat toisiaan pisteessä (1, 3).Tehtävä 263
Määritä pisteen (-4, ) kautta kulkevien käyrän 9y = x2 normaalien
yhtälöt.
) kautta kulkevien käyrän 9y = x2 normaalien
yhtälöt.
Tehtävä 264
Osoita implisiittistä derivointia käyttäen, että yhtälönx5 + x3y3 + y5 = 1
määrittelemällä käyrällä on ainakin yksi vaakasuora ja yksi pystysuora tangentti. Missä käyrän pisteissä nämä sijaitsevat? Piirrä kuvio.
Tehtävä 265
Yhtälö xy = yx määrittää käyrän ainakin joillakin arvoilla x. Osoita, että piste (2, 4) sijaitsee tällä käyrällä ja määritä tähän pisteeseen asetetun käyrän tangentin kulmakerroin. Piirrä käyrä.Tehtävä 266
Laske käyrien y =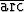 sin x ja y =
sin x ja y =  cos x tangenttien välinen kulma käyrien
leikkauspisteessä.
cos x tangenttien välinen kulma käyrien
leikkauspisteessä.
Tehtävä 267
Määritä arvoa x = a vastaaviin käyrien y = sinh x ja y = cosh x pisteisiin asetettujen a) tangenttien, b) normaalien leikkauspisteet.7.2 Ääriarvotehtävät
Tehtävä 268
Määritä seuraavien funktioiden suhteelliset ja absoluuttiset ääriarvot; piirrä kuvaajat:| a) 1 - 6x + 9x2 - 5x3, | b)  , , | ||||||
c) 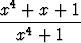 , , | d)  . . |
Tehtävä 269
Määritä seuraavien funktioiden maksimi ja minimi annetulla välillä:| a) (x + 1)3(x - 3)3, [-2, 4], | |||
| b) |x5 - 80x + 1|, [-1, 1], | |||
c)  , [-100, 2]. , [-100, 2]. |
Tehtävä 270
Tutki, millä vakion a arvoilla funktiolla
f(x) = 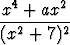
on sellainen ominaisuus, että eräällä muuttujan x arvolla se saa absoluuttisen maksimiarvonsa.
Tehtävä 271
Olkoot x ja y kaksi ei-negatiivista lukua, joiden summa on . Määritä
lausekkeen x
. Määritä
lausekkeen x +
+  suurin ja pienin mahdollinen arvo.
suurin ja pienin mahdollinen arvo.
Tehtävä 272
Määritä funktion
f(x) = (sin x)sin x, x  ]0,
]0,  [,
[,
pienin yläraja (supremum) ja suurin alaraja (infimum).
Tehtävä 273
Kolmannen asteen Tshebyshevin polynomin T3(x) lauseke voidaan välillä [-1, 1] esittää muodossa T3(x) = cos(3 cos x). Esitä lauseke muodossa
ax3 + bx2 + cx + d ja määritä polynomin suurin ja pienin arvo välillä [-1, 1].
cos x). Esitä lauseke muodossa
ax3 + bx2 + cx + d ja määritä polynomin suurin ja pienin arvo välillä [-1, 1].
Tehtävä 274
Olkoot x ja y kaksi positiivista lukua, joiden summa on 18. Määritä lausekkeelle x4 + y2 supremum, infimum, maksimi ja minimi, mikäli tällainen on olemassa.Tehtävä 275
Määritä niistä lieriöistä, jotka voidaan piirtää R-säteisen pallon sisään, a) tilavuudeltaan, b) vaipaltaan, c) kokonaispinta-alaltaan suurin.Tehtävä 276
Tasakylkisen kolmion kannan pituus on 12 ja huipusta piirretyn
korkeusjanan pituus 11. Tältä korkeusjanalta on valittu piste P siten, että siitä kolmion
kärkiin piirrettyjen etäisyyksien summa on mahdollisimman pieni. Missä suhteessa P
jakaa korkeusjanan?
ja huipusta piirretyn
korkeusjanan pituus 11. Tältä korkeusjanalta on valittu piste P siten, että siitä kolmion
kärkiin piirrettyjen etäisyyksien summa on mahdollisimman pieni. Missä suhteessa P
jakaa korkeusjanan?
Tehtävä 277
Suorakulmion yhtenä kärkenä on käyrän(ax)2/3 + y2/3 = b2/3
piste P ja muina kärkinä pisteen P :n symmetriapisteet x-akselin, y-akselin ja origon suhteen. Määritä suorakulmion pinta-alan ääriarvot, kun P liikkuu ko. käyrällä.
Tehtävä 278
Ympyrän sektorin piiri olkoon vakio = p. Tutki pinta-alan ääriarvoja.Tehtävä 279
Kolmion kahden sivun välinen jana puolittaa kolmion alan. Tutki janan pituuden ääriarvoja.Tehtävä 280
On valmistettava lieriö, jonka tilavuus on vakio v m3. Pohjat maksavat a mk /m 2 ja vaippa b mk/m2. Tutki hinnan ääriarvoja.Tehtävä 281
Määritä annetun ympyrän segmentin sisään piirretyn alaltaan suurimman suorakulmion sivujen pituudet.Tehtävä 282
Suoran qy = m2 ja paraabelin qy = x2 (m, q positiivisia) rajoittamaan alueeseen asetetaan puolisuunnikas, jonka yhdensuuntaiset sivut ovat x-akselin suuntaiset. Miten suuri puolisuunnikkaan ala voi enintään olla?Tehtävä 283
Suoran ympyräkartion pohjaympyrän keskipiste on kiinteän suoran lieriön pohjaympyrän keskipisteessä ja kartion huippu on lieriön toisen pohjaympyrän keskipisteessä. Määritä kartion ja lieriön pohjien säteiden suhde siten, että kartion ulkopuolelle jäävän lieriön osan ja lieriön ulkopuolelle jäävän kartion osan tilavuuksien summa on mahdollisimman pieni.Tehtävä 284
Suora ympyräkartio asetetaan pallon sisään siten, että kartion huippu ja pohjaympyrän kehä sijaitsevat pallon pinnalla. Miten monta prosenttia kartion tilavuus voi enintään olla pallon tilavuudesta? Vastaus prosenttiyksikön tarkkuudella.Tehtävä 285
Kuvioon, jota rajoittavat x-akseli ja käyrä y = 12 + 4x - x2, piirretään kolmio ABC siten, että piste A on origossa, pisteet B ja C käyrällä sekä sivu BC x-akselin suuntainen. Millä etäisyydellä sivun BC on oltava x-akselista, jotta kolmion ala olisi mahdollisimman suuri?Tehtävä 286
Käyrälle y = sin x piirretään muuttujan arvoja x0 ja x0 + 2 vastaaviin
pisteisiin tangentit ja normaalit. Määritä niiden rajoittaman suorakulmion alan maksimi-
ja minimiarvo.
vastaaviin
pisteisiin tangentit ja normaalit. Määritä niiden rajoittaman suorakulmion alan maksimi-
ja minimiarvo.
Tehtävä 287
Olkoon suorakulmaisessa kolmiossa muuttuvan terävän kulman viereinen kateetti vakio = a, vastainen kateetti b = b(
viereinen kateetti vakio = a, vastainen kateetti b = b( ) ja hypotenuusa c = c(
) ja hypotenuusa c = c( ).
Millä muuttujan
).
Millä muuttujan  arvolla lauseke 2c(
arvolla lauseke 2c( ) -
) -  b(
b( ) saa mahdollisimman pienen
arvon?
) saa mahdollisimman pienen
arvon?
Tehtävä 288
Suoran tien varressa on kohtisuorassa tien suuntaa vastaan mainostaulu, jonka leveys on 10 metriä ja etäisyys tiestä 20 metriä. Määritä suurin (vaakasuoran tason) kulma, jossa tiellä liikkuja taulun näkee. (Tien leveyttä ei oteta huomioon.)Tehtävä 289
Olkoon annettuna pisteet A (1, 0) ja B
(1, 0) ja B  (t, 0), missä t > 1. Piste C sijaitsee
positiivisella y-akselilla site, että kulma
(t, 0), missä t > 1. Piste C sijaitsee
positiivisella y-akselilla site, että kulma  ACB =
ACB =  on mahdollisimman suuri. Määritä t
siten, että kulman
on mahdollisimman suuri. Määritä t
siten, että kulman  maksimiarvo on
maksimiarvo on  /4.
/4.
Tehtävä 290
Määritä sen kolmion pinta-alan suhteelliset ja absoluuttiset ääriarvot, jota rajoittavat käyrän y = ln x pisteeseen piirretty normaali, tähän pisteeseen piirretty pystysuora ja x-akseli.Tehtävä 291
Olkoon x
 ja olkoon i imaginaariyksikkö. Osoita, että funktiolla
f(x) = |x - i| + |x - 1 - 2i| on absoluuttinen minimi ja määritä sen arvo. Mikä on
tehtävän geometrinen tulkinta?
ja olkoon i imaginaariyksikkö. Osoita, että funktiolla
f(x) = |x - i| + |x - 1 - 2i| on absoluuttinen minimi ja määritä sen arvo. Mikä on
tehtävän geometrinen tulkinta?
Tehtävä 292
Osoita, että sin x > 2x/ , kun x
, kun x  [0,
[0,  /2].
/2].
Tehtävä 293
Todista: a) ex > ex kaikilla x
 ; b) ex > 1 + x + x2/2 kaikilla x > 0.
; b) ex > 1 + x + x2/2 kaikilla x > 0.
Tehtävä 294
Millä arvoilla a
 on voimassa
on voimassa
(ex+a + e-x)2 > 4(a + 1) kaikilla x 
 ?
?
Tehtävä 295
Osoita, että x - ln x - 1 > 0, kun x > 0. Osoita tämän avulla, että jos positiivilukujen x1, x2, . . . , xp summa on = p, niin lukujen tulo on < 1.7.3 Derivaatta nopeutena
Tehtävä 296
Piste P liikkuu pitkin x-akselia negatiiviseen suuntaan vakionopeudella v1 ja piste Q pitkin y-akselia negatiiviseen suuntaan vakionopeudella v2. Hetkellä t = 0 piste P on kohdassa (a, 0) ja Q kohdassa (0, b) (a > 0, b > 0). Millä hetkellä välimatka P Q on lyhin? Mikä on lyhin välimatka?Tehtävä 297
Talon korkeus on 25 metriä. Sen katolta pudotetaan kivi ilman alkunopeutta ja yhtä sekuntia myöhemmin toinen kivi alkunopeudella v0. Kuinka v0 on valittava, jotta kivet putoaisivat maahan samanaikaisesti? (Ilmanvastus voidaan jättää huomiotta.)Tehtävä 298
Mies heittää sillalta kiven suoraan ylöspäin. Kolmen sekunnin kuluttua kivi ohittaa pudotessaan miehen ja kahden sekunnin kuluttua tästä putoaa veteen. Mikä oli kiven saama alkunopeus ja mikä sillan korkeus?Tehtävä 299
Astronautti pudottaa kiven kallionkielekkeeltä ja toteaa sen putoavan kolmessa sekunnissa alas kallion juurelle. Kuinka korkea kallio on, jos ollaan a) Marsissa (g = 3.8 m /s 2 ), b) Saturnuksessa (g = 11.5 m/s2)?Tehtävä 300
Edellisen tehtävän astronautin kumppani on kallion juurella ja heittää kiven takaisin, jotta koe voitaisiin toistaa. Mikä on pienin alkunopeus, mitä hänen on käytettävä a) Marsissa, b) Saturnuksessa?Tehtävä 301
Santaa valutetaan kartionmuotoiseen kasaan nopeudella 0.2 m3/min. Kitka säilyttää kartion pohjan säteen suhteen korkeuteen vakiona . Mikä on korkeuden
kasvunopeus, kun pohjan säde on 2 m?
. Mikä on korkeuden
kasvunopeus, kun pohjan säde on 2 m?
Tehtävä 302
Kuution pinta-ala kasvaa nopeudella 50 cm2/s. Mikä on tilavuuden kasvunopeus, kun särmän pituus on 20 cm?Tehtävä 303
Tietyllä ajanhetkellä pallon säde on 3 cm ja pallon tilavuus kasvaa nopeudella 2 cm3/s. Millä nopeudella kasvaa pallon ala?Tehtävä 304
Suoralla ympyräkartiolla on puolen kuutiometrin vakiotilavuus. Pohjan säde kasvaa vakionopeudella 10 cm/s, jolloin kartion korkeus vastaavasti pienenee. Määritä pienenemisnopeus kartion korkeuden ollessa 100 cm.Tehtävä 305
Miehen pituus on 180 cm. Hän lähtee kävelemään 6 metrin korkeudella olevan katulyhdyn alta vakionopeudella 1 m/s. Mikä on miehen varjon pituuden muuttumisnopeus, kun hän on kulkenut a) 3 metriä, b) 15 metriä? Mikä on varjon kärjen nopeus?Tehtävä 306
Lentokone lentää vaakasuorasti 600 metrin korkeudessa vakionopeudella 600 km/t suoraan katselijan yli. Olkoon pystysuunnan ja näkösäteen välinen kulma.
Laske kulman
pystysuunnan ja näkösäteen välinen kulma.
Laske kulman  muuttumisnopeus, kun a)
muuttumisnopeus, kun a)  = 45o, b)
= 45o, b)  = 0o. Milloin nopeus on
suurimmillaan?
= 0o. Milloin nopeus on
suurimmillaan?
Tehtävä 307
Lausu eksentrisyyden e funktiona se kulma , jossa ellipsin polttopisteiden
etäisyys näkyy pikkuakselin päätepisteestä. Ellipsi muuttaa ajan t kuluessa jatkuvasti
muotoaan siten, että
, jossa ellipsin polttopisteiden
etäisyys näkyy pikkuakselin päätepisteestä. Ellipsi muuttaa ajan t kuluessa jatkuvasti
muotoaan siten, että  on vakio = p. Laske kulman
on vakio = p. Laske kulman  muuttumisnopeus hetkellä, jolloin
e = 4/5.
muuttumisnopeus hetkellä, jolloin
e = 4/5.
7.4 Yhtälön iteratiivinen ratkaiseminen
Tehtävä 308
Etsi Newtonin menetelmällä polynomin x3 + 8x2 - 44x - 10 kaikki nollakohdat.Tehtävä 309
Tutki kokeilemalla, voidaanko polynomin x3 + 8x2 - 44x - 10 nollakohdat löytää iteraatiolla xn+1 = (x
(x + 8x
+ 8x - 10). Miten tämä iteraatiokaava on muodostettu?
- 10). Miten tämä iteraatiokaava on muodostettu?
Tehtävä 310
Etsi yhtälön x = cos x ratkaisu 10 desimaalin tarkkuudella käyttäen iteraatiota xn+1 = cos xn. Onnistuuko ratkaisu iteraatiolla xn+1 = cos xn?
cos xn?
7.5 L’Hospitalin sääntö
Tehtävä 311
Tarkista, että yleistettyä väliarvolausetta voidaan soveltaa osamäärään f/g seuraavissa tapauksissa ja määritä väliarvot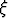 :
:
a) f(x) = cos 2x, g(x) = sin x, väli [0, 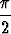 ]; ]; | |||
| b) f(x) = sinh x, g(x) = cosh x, väli [0, 6]; | |||
| c) f(x) = x2, g(x) = x3, väli [1, 2]; | |||
| d) f(x) = 4 - x2, g(x) = x3 - 3x, väli [-3, 2]. |
Tehtävä 312
Yleistettyä väliarvolausetta yritetään soveltaa osamäärään f/g seuraavissa tapauksissa:| a) f(x) = x2, g(x) = x3, väli [-2, 3]; | |||
| b) f(x) = 3 + (x - 2)(x - 1)2, g(x) = 1 + x(x - 1)2, väli [0, 2]. |
Totea, että väliarvoa 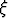 ei voida löytää. Onko lause virheellinen?
ei voida löytää. Onko lause virheellinen?
Tehtävä 313
Määritä l’Hospitalin sääntöä käyttäen raja-arvota) limx  /4 /4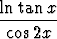 , , | b) limx 0 0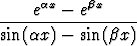 , , | c) limx 0 0 , , | |||||||||
d) limx 4 4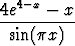 , , | e) limx 0 0 , , | f) limx 0 0 . . |
Suorita myös numeerisia kokeiluja.
Tehtävä 314
Määritä seuraavat raja-arvot l’Hospitalin sääntöä käyttäen:
a) limx
 x2 ln(cos
x2 ln(cos 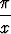 ), b) limx
), b) limx
 x(a1/x - 1) (a > 0), c) limx
x(a1/x - 1) (a > 0), c) limx

 .
.
Tehtävä 315
Määritä seuraavat raja-arvot l’Hospitalin sääntöä käyttäen:
a) limx

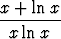 , b) limx
, b) limx

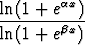 (
( > 0,
> 0,  > 0), c) limx
> 0), c) limx 0+ sin x ln x.
0+ sin x ln x.
Tehtävä 316
Määritä seuraavat raja-arvot:a) limx  /2(sin x)tan x, /2(sin x)tan x, | b) limx 0+x3e1/x, 0+x3e1/x, | c) limx 0(1 + x3)4/x3
, 0(1 + x3)4/x3
, | d) limx  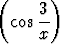 x, x, | ||||||||||||
e) limx 0+xln (1+x), 0+xln (1+x), | f) limx 0+(ex - 1)sin x, 0+(ex - 1)sin x, | g) limx 0+(tan x)sin x, 0+(tan x)sin x, | h) limx  (1 + 2x)e-x
. (1 + 2x)e-x
. |
Suorita myös numeerisia kokeiluja.
Tehtävä 317
Määritä l’Hospitalin säännön avulla raja-arvot
a) limx 0
0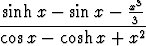 , b) limx
, b) limx
 (sin x)tan 2
x.
(sin x)tan 2
x.
Tehtävä 318
Olkoon f(x) = x + sin x, g(x) = x. Todista, että
limx

 = 1, mutta limx
= 1, mutta limx

 ei ole olemassa.
ei ole olemassa.
Miksi l’Hospitalin sääntöä ei voi käyttää?
Tehtävä 319
Todista, että jos funktio f on derivoituva ja limx
 (f(x) + f'(x)) = A, niin
limx
(f(x) + f'(x)) = A, niin
limx
 f(x) = A ja limx
f(x) = A ja limx
 f'(x) = 0.
f'(x) = 0.