8 Vektoriarvoiset funktiot
8.1 Vektoriarvoisen funktion jatkuvuus ja derivoituvuus
Tehtävä 320
Olkoon u reaalimuuttujan vektoriarvoinen funktio
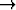
n ja limt
au(t) = b.
Todista: limta||u(t)|| = ||b||.
Tehtävä 321
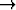
Olkoon u reaalimuuttujan vektoriarvoinen funktio n ja limtau(t) = b,
missä b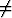
o. Todista:
limta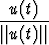
= 
.
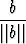Tehtävä 322
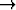
Olkoon u reaalimuuttujan vektoriarvoinen funktio n. Osoita, että
vaikka funktio ||u(t)|| olisikin derivoituva, ei funktio u(t) välttämättä ole.
Tehtävä 323
Laske u'(t), |u'(t)|, u''(t) ja |u''(t)| arvolla t = 0, kun
a) u(t) = (t3 + 2t) i - 3e-2t j + 2 sin 5t k, b) u(t) = ln(t2 + 1) i +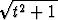 
j + 
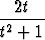k.
Tehtävä 324
Olkoon u(t) neljästi derivoituva vektorifunktio. Laske ensimmäinen ja toinen derivaatta skalaarikolmitulolle [u(t), u'(t), u''(t)].Tehtävä 325
Olkoon u(t) derivoituva vektorifunktio ja u(t)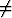
o. Osoita:
u0(t) ×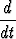 
u0(t) = 
× 
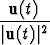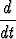u(t).
Tehtävä 326
Olkoon e(t) kahdesti derivoituva yksikkövektori ja e''(t)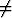
o kaikilla
muuttujan t arvoilla. Osoita, että vektoreiden e(t) ja e''(t) välinen kulma ei koskaan ole
terävä.
Tehtävä 327
Olkoot u(t) ja v(t) vektorifunktioita. Osoita, että jos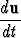
= w × u ja
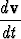= w × v, niin 
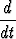(u × v) = w × (u × v).
Tehtävä 328
Olkoon u(t) derivoituva vektorifunktio ja a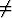
o vakiovektori. Osoita:
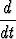comp(u, a) = comp 
,
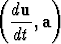missä comp (u, a) tarkoittaa vektorin u skalaarikomponenttia vektorin a suunnalle.
Tehtävä 329
Olkoot a ja b kaksi lineaarisesti riippumatonta vakiovektoria ja olkoon r(t) = a cos t + b sin t. Osoita, että [r(t), r'(t), r''(t)] = 0 kaikilla muuttujan t arvoilla. Jos t on aika ja r(t) esittää liikkuvan pisteen paikkavektoria, niin mikä on väitteen geometrinen tulkinta?Tehtävä 330
Osoita, että yhtälö z - p sin z = t määrittää funktion z = z(t), kun p on vakio ja |p| < 1. Näytä, että tämän funktion avulla määritelty vektorifunktio
r(t) = (cos z(t) - p) i +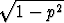 
sin z(t) j
toteuttaa differentiaaliyhtälön r''(t) = -r(t)/|r(t)|3.
8.2 Taso- ja avaruuskäyrät
Tehtävä 331
Tutki, onko piste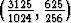
käyrällä
x =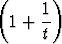 
t+1, y = 
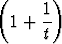t.
Miten käyrä käyttäytyy, kun t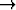 
?
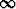Tehtävä 332
Määritä käyränkaaren r(t) =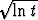
i + (1/t) j, t 
[1, 3], pisteiden suurin ja
pienin etäisyys origosta. Piirrä kuvio.
Tehtävä 333
Osoita, että kun ympyrä vierii liukumatta suoraa pitkin, sen kehällä oleva piste piirtää sykloidin.Tehtävä 334
Määritä avaruuskäyrän r(t) = t3 i + t2 j + t k yksikkötangenttivektori pisteessä (8, 4, 2).Tehtävä 335
Laske ruuviviivan r(t) = a cos t i + a sin t j + bt k tangenttivektori pisteessä, joka vastaa parametriarvoa t0. Laske tähän pisteeseen asetetun ruuviviivan normaalitason yhtälö muodossa
x + 
y + 
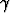z =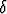 
. Mikä on tämän tason lyhin etäisyys
origosta?
Tehtävä 336
Määritä neljän desimaalin tarkkuudella ruuviviivan
r(t) = cos t i + sin t j +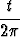 
k
sen pisteen P koordinaatit, joka on lähinnä pistettä (0, 1, 0). Perustele ääriarvon laatu geometrisen havainnon avulla. Pisteeseen P asetetaan ruuviviivan tangentti; määritä tangentin ja xy-tason leikkauspiste.
Tehtävä 337
Osoita, että r(t) = a cosh t i + b sinh t j (a > 0, b > 0) esittää hyperbelin toista haaraa. Osoita, että käyrä on sileä ja säännöllinen. Millä parametrin t arvolla käyrän tangentti on y-akselin suuntainen?Tehtävä 338
Määritä käyrän r(t) = a(cos t + t sin t) i + a(sin t - t cos t) j normaalin etäisyys origosta.Tehtävä 339
Piirrä käyrä r = (cos t + t sin t)i + (sin t - t cos t)j.Tehtävä 340
Piirrä käyrä r(t) = cos(5t) i + sin(6t) j, t [0, 2
].
Tehtävä 341
Piirrä käyrä
r(t) =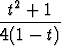 
i + 
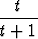j
ja määritä sen (suoraviivaiset) asymptootit sekä pisteet, joissa tangentti on vaaka- tai pystysuora.
Tehtävä 342
Piirrä käyrä
r(t) =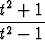 
i + 
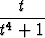j
ja määritä sen (suoraviivaiset) asymptootit sekä pisteet, joissa tangentti on vaaka- tai pystysuora.
Tehtävä 343
Piirrä käyrä
r(t) =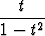 
i + 
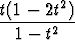j
ja määritä sen (suoraviivaiset) asymptootit sekä pisteet, joissa tangentti on vaaka- tai pystysuora.
Tehtävä 344
Piirrä käyrä
r(t) =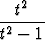 
i + 
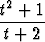j
ja määritä sen (suoraviivaiset) asymptootit sekä pisteet, joissa tangentti on vaaka- tai pystysuora.
Tehtävä 345
Piirrä napakoordinaattikäyrät r = | sin n
|, n = 1, 2, 3.
Tehtävä 346
Napakoordinaateissa annettu käyrä r = a(1 + cos) on kardioidi. Missä
pisteissä käyrän tangentti on x- tai y-akselin suuntainen? Piirrä käyrä.
Tehtävä 347
Osoita, että kardioidi r = 1 + cos ja kardioidi r = 1 - cos leikkaavat
toisensa kohtisuorasti.
Tehtävä 348
Määritä suorakulmaiset koordinaatit viiden desimaalin tarkkuudella sille kardioidin r = 1 + cos pisteelle, joka sijaitsee lähinnä pistettä x = y = 1.
Tehtävä 349
Tutki napakoordinaattikäyrän r = a sin 3 pisteeseen osoittavan
paikkavektorin ja tähän pisteeseen asetetun tangenttivektorin välistä kulmaa muuttujan
eri arvoilla. Piirrä käyrä.
Tehtävä 350
Arkhimedeen spiraali määritellään napakoordinaattiyhtälöllä r = a. Tutki
käyrän pisteeseen osoittavan paikkavektorin ja tähän pisteeseen asetetun tangenttivektorin
välistä kulmaa muuttujan eri arvoilla. Piirrä käyrä.
Tehtävä 351
Logaritminen spiraali määritellään napakoordinaattiyhtälöllä r = aek
.
Tutki käyrän pisteeseen osoittavan paikkavektorin ja tähän pisteeseen asetetun
tangenttivektorin välistä kulmaa muuttujan eri arvoilla. Piirrä käyrä sopivilla lukujen a
ja k arvoilla.
Tehtävä 352
Piirrä Arkhimedeen spiraali r = ja logaritminen spiraali r = e. Määritä
suuntaa = lähellä olevan käyrien leikkauspisteen napakoordinaatit numeerisesti.
Määräytyykö leikkauspiste yksikäsitteisesti em. ehdosta?
Tehtävä 353
Piirrä konkoidi r = a sin 3(/3). Olkoon käyrän tangenttivektorin ja
x-akselin välinen kulma, käyrän pisteen paikkavektorin ja tähän pisteeseen asetetun
tangenttivektorin välinen kulma. Lausu kulmat parametrin funktioina ja tutki niiden
suhdetta toisiinsa.
Tehtävä 354
Yhtälö x3 + y3 - axy = 0 esittää käyrää, jota kutsutaan Cartesiuksen lehdeksi. Johda käyrälle parametriesitys, jossa parametrina on käyrän pisteen ja origon määräämän suoran kulmakerroin t; ts. tee yhtälöön sijoitus y = xt. Piirrä käyrä.Tehtävä 355
Johda Pascalin simpukan (x2 + y2 - 4x)2 = 16(x2 + y2) napakoordinaattiyhtälö ja piirrä käyrä.Tehtävä 356
Johda Bernoulli’n lemniskaatan (x2 + y2)2 = 2(x2 - y2) napakoordinaattiyhtälö ja piirrä käyrä.Tehtävä 357
Määritä käyrän x2y - xy2 + 16 = 0 vaakasuorat ja pystysuorat tangentit implisiittisen derivoinnin avulla. Piirrä käyrä.Tehtävä 358
Todista, että yhtälöpari x =
t3 + t, y = et määrittelee kaikilla arvoilla
x jatkuvan funktion y = f(x). Piirrä funktion kuvaaja sekä määritä sen ääriarvot ja
käännepisteet.
Tehtävä 359
Tutki, määritteleekö yhtälöpari x = t - sin t cos t, y = t2 funktion y = f(x).Tehtävä 360
Laske yhtälöparin x = t - sin t cos t, y = t2 määrittämän funktion y = f(x) ensimmäinen ja toinen derivaatta parametrin t funktiona.Tehtävä 361
Osoita, että yhtälöiden
x =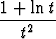 
, y =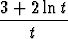 
(t > 0)
määrittämä funktio y(x) toteuttaa differentiaaliyhtälön
y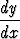
= 2x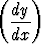
2 + 1.
Piirrä funktion y(x) kuvaaja. Millä muuttujan x arvoilla funktio on määritelty? Mitä muuta funktiosta voidaan sanoa?
Tehtävä 362
Olkoon r0 = i + 2j + 3k, a =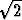
(i + j + k), b = 
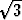(i - k). Tutki,
minkälainen käyrä on
r(t) = r0 + (cos t)a + (sin t)b, t [0, 2].
Mitä käyriä ovat tämän käyrän ortogonaaliprojektiot koordinaattitasoille?
Tehtävä 363
Tutki, millainen avaruuskäyrä on kyseessä, kun
r(t) = ln(t + 1) (cos t i + sin t j) +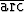 
tan t k, t > 0.
Piirrä käyrän projektiot koordinaattitasoille.
Tehtävä 364
Tutki heittoliikettä: Miten lähtönopeuden muutos vaikuttaa heittoetäisyyteen ja lentoradan maksimikorkeuteen?Tehtävä 365
Osoita, että vinossa heittoliikkeesä heittoetäisyys on suurimmillaan, kun korotuskulma on 45o.Tehtävä 366
Liikkuvan partikkelin paikkavektori r = r(t) toteuttaa yhtälön
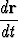= a + b × r0,
missä a ja b ovat vakiovektoreita. Osoita, että r toteuttaa myös yhtälön
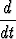(r × a + |r|b) = 
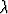r0,
missä 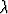on eräs vakio. Määritä .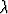