9 Määrätty integraali
9.1 Riemannin – Darboux’n ylä- ja alasummat
Tehtävä 368
Tarkastellaan funktiota f(x) = x välillä [0, 1] ja tämän välin jakoa p = {0, a, 1}, missä 0 < a < 1. Määritä alasumma Sp ja yläsumma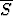 p. Määritä sup S p ja
inf
p. Määritä sup S p ja
inf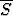 pem. tyyppiä oleville jaoille. Seuraako saatujen lukujen erisuuruudesta, että että
funktio f ei ole integroituva välillä [0, 1]?
pem. tyyppiä oleville jaoille. Seuraako saatujen lukujen erisuuruudesta, että että
funktio f ei ole integroituva välillä [0, 1]?
Tehtävä 369
Olkoon p välin [a, b] jako, jossa on n osaväliä. Osoita: |p|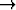 0
0 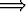 n
n 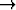
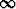 .
Onko käänteinen implikaatio tosi?
.
Onko käänteinen implikaatio tosi?
Tehtävä 370
Olkoon funktio f rajoitettu välillä [a, b] ja integroituva jokaisella välillä [a, c], missä a < c < b. Todista, että f on integroituva välillä [a, b].Tehtävä 371
Todista, että jos funktio f on integroituva suljetulla välillä [a, b], niin se on integroituva myös jokaisella tämän välin suljetulla osavälillä.Tehtävä 372
Olkoon funktio f rajoitettu välillä [a, b]. Oletetaan, että on olemassa vakio K > 0 siten, että kaikille välin [a, b] jaoille p, joissa on n osaväliä, pätee
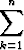 (Gk - gk) < K.
(Gk - gk) < K.
Tässä Gk ja gk ovat funktion arvojen pienin yläraja ja suurin alaraja k:nnella osavälillä. Todista, että tällöin f on integroituva välillä [a, b].
9.2 Riemannin summa
Tehtävä 373
Laske seuraavat integraalit muodostamalla Riemannin summan raja-arvo:
a) 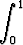 x2 dx, b)
x2 dx, b) 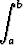 x2 dx.
x2 dx.
Ohjeeksi kaava 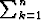 k2 =
k2 =  n(n + 1)(2n + 1).
n(n + 1)(2n + 1).
Tehtävä 374
Laske seuraava integraali muodostamalla Riemannin summan raja-arvo:
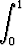 ex dx.
ex dx.
Tehtävä 375
Välille [a, b] muodostetaan tasavälinen jako, jossa on n osaväliä, ja aidosti kasvavan funktion f integraalia approksimoidaan vastaavalla Riemannin summalla. Kuinka suureksi on n valittava, jotta approksimointivirheen itseisarvo olisi < ?
?
Tehtävä 376
Olkoon f rajoitettu funktio, joka on välillä [-a, a] integroituva. Todista, että jos f on parillinen, niin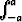 f = 2
f = 2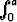 f, ja jos f on pariton, niin
f, ja jos f on pariton, niin 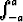 f = 0.
f = 0.
9.3 Määrätyn integraalin perusominaisuudet
Tehtävä 377
Osoita, että
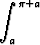 sin 2x dx
sin 2x dx
ei riipu luvusta a.
Tehtävä 378
Olkoon funktio f integroituva suljetulla välillä I ja a I. Todista, että
funktio
I. Todista, että
funktio
H(x) = 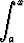 f
f
on jatkuva välillä I.
Tehtävä 379
Laske
a) 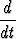
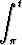 sin3u du, b)
sin3u du, b) 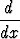
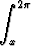 (sin 2t - t4e-t) dt, c)
(sin 2t - t4e-t) dt, c) 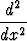
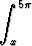 (sin x)(ex)(ln x) dx (x > 0).
(sin x)(ex)(ln x) dx (x > 0).
Tehtävä 380
Laske
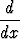
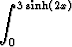
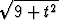 dt.
dt.
Tehtävä 381
Piirrä funktion
F (x) = 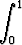 |t - x| dt
|t - x| dt
kuvaaja. Mikä on funktion pienin arvo?
Tehtävä 382
Olkoon funktio f jatkuva välillä [a, b]. Mikä on funktion
g(x) = 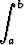 [f(t) - x]2 dt
[f(t) - x]2 dt
minimiarvo ja millä muuttujan arvolla tämä saadaan?
Tehtävä 383
Laske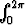 f(x) dx, kun f'(x) = | sin x| ja f(0) = 1.
f(x) dx, kun f'(x) = | sin x| ja f(0) = 1.
Tehtävä 384
Tulkitse seuraava lauseke Riemannin summien raja-arvoksi, palauta se integraaliksi ja laske:
limn

![[13 23 (4n - 1)3]
-4-+ -4-+ ...+ -----4----
n n n](kuvat/ra813x.gif) .
.
Tehtävä 385
Tulkitse seuraavat lausekkeet Riemannin summien raja-arvoiksi, palauta ne integraaleiksi ja laske:
a) limn

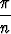
 sin
sin 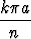 , b) limn
, b) limn

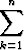
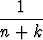 .
.
Tehtävä 386
Onko seuraava lasku oikein?
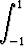
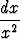 =
= 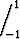 -
-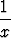 = -2.
= -2.
Tehtävä 387
Laske seuraavat integraalit:
a) 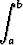 (a + bx) dx, b)
(a + bx) dx, b) 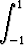 (ax2 + bx + c) dx, c)
(ax2 + bx + c) dx, c) 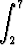
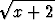 dx.
dx.