10 Integroimistekniikkaa
10.1 Integraalifunktio
Tehtävä 388
Vertaa funktioiden a) ln x ja ln 10x, b)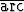 tan x ja
tan x ja 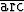 tan
tan 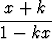 ,
c) ln (x +
,
c) ln (x + 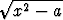 ) ja - ln(x -
) ja - ln(x - 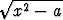 ), missä a > 0, derivaattoja toisiinsa. Tutki
funktioiden erotusta muuttujan eri arvoilla.
), missä a > 0, derivaattoja toisiinsa. Tutki
funktioiden erotusta muuttujan eri arvoilla.
Tehtävä 389
Sievennä lauseke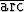 sin(2x
sin(2x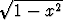 ) muodostamalla ensin sen derivaatta.
) muodostamalla ensin sen derivaatta.
Tehtävä 390
Määritä se funktion 2x - 3 integraalifunktio, jonka kuvaaja sivuaa suoraa x + y = 0.Tehtävä 391
Käyrä y = f(x) kulkee pisteen (3, 1) kautta ja jokaisessa pisteessä (x, f(x)) tangentin kulmakerroin on x2 + 2x. Määritä käyrän yhtälö.Tehtävä 392
Onko funktiolla |x| integraalifunktiota, joka on määritelty kaikilla x
 ?
?
Tehtävä 393
Määritä se funktion f(x) = x + |x| integraalifunktio F , joka toteuttaa ehdon F (1) = 2. Todenna, että F '(0) = f(0). Laske F (-2).Tehtävä 394
Määritä seuraavien funktioiden integraalifunktiot a) käsin laskulla, b) jotakin tietokoneohjelmaa käyttäen:a) x3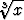 , , | b) 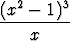 , , | c) 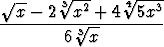 , , | |||||||||
d) 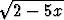 , , | e) (3x - 7)413, | f) (2x2 - 5x + 7)(4x - 5), | |||||||||
g) 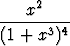 , , | h) 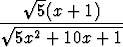 , , | i) sin x sin 2x, | |||||||||
j) 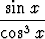 , , | k) 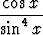 , , | l) 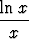 , , | |||||||||
m) 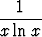 , , | n) ex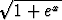 , , | o) 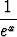 , , | |||||||||
p) e3x + 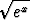 , , | q) 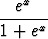 , , | r) 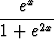 , , | |||||||||
s) 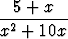 , , | t) 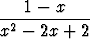 , , | u) 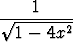 , , | |||||||||
v) 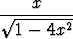 , , | w) 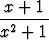 , , | x) 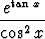 , , | |||||||||
y) 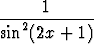 , , | z) 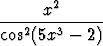 , , | å) sinh 2x, | |||||||||
| ä) cosh 2x, | ö) 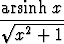 . . |
Tehtävä 395
Etsi seuraaville funktioille f annetun ehdon täyttävä integraalifunktio F :a) f(x) = 4 sin x cos x - 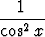 , F (0) = 2, , F (0) = 2, | |||
b) f(x) = 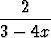 , F ( , F (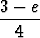 ) = 0, ) = 0, | |||
c) f(x) = -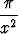 cos cos 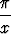 , F (1) = 0. , F (1) = 0. |
Tehtävä 396
Laske seuraavat määrätyt integraalit:
a) 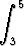
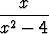 dx, b)
dx, b) 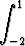
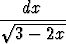 , c)
, c) 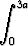
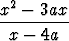 dx (a
dx (a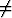 0).
0).
10.2 Sijoitusmenettely
Tehtävä 397
Suorita jokin sopivalta tuntuva sijoitus, kun integroitava on muotoa
a) 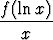 , b) f(cos x) sin x, c) f(tan x) cos 2x, d) f(aex + b)ex (a, b vakioita).
, b) f(cos x) sin x, c) f(tan x) cos 2x, d) f(aex + b)ex (a, b vakioita).
Miten integraali muuntuu kussakin tapauksessa?
Tehtävä 398
Laske seuraavat integraalit sijoitusta käyttäen:a) 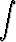 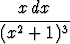 , , | b) 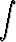 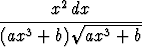 , , | c) 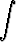 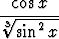 dx, dx, | |||||||||
d) 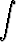 (1 + tan 2x) (1 + tan 2x)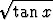 dx, dx, | e) 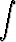 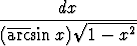 , , | f) 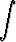 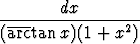 , , | |||||||||
g) 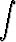 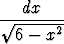 , , | h) 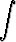 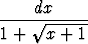 . . |
Tehtävä 399
Laske integraali
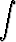
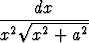
a) sijoituksella x = 1/t, b) sijoituksella x = a tan t, c) sijoituksella x = a sinh t.
Tehtävä 400
Etsi funktion 1/ cosh x integraalifunktio a) sijoituksella t = ex, b) sijoituksella t = tanh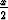 . Vertaa saatuja integraalifunktioita.
. Vertaa saatuja integraalifunktioita.
Tehtävä 401
Määritä ne funktion
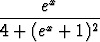
integraalifunktiot, joiden kuvaajilla on asymptoottina x-akseli.
Tehtävä 402
Muodosta sijoitusmenettelyä käyttäen seuraavista integraaleista kustakin kolme uutta integraalia, jotka eivät ole integroitavissa alkeisfunktioiden avulla:
a) 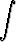
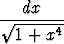 , b)
, b) 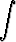 ex2
dx, c)
ex2
dx, c) 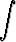
 dx, d)
dx, d) 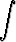
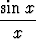 dx, a)
dx, a) 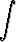
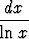 .
.
Tehtävä 403
Laske seuraavat määrätyt integraalit sijoitusta käyttäen:
a) 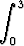
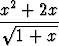 dx, b)
dx, b) 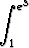
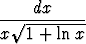 .
.
Tehtävä 404
Osoita, että jos f on jatkuva funktio ja a < b, niin integraali
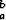 f(x) dx
voidaan muuntaa muotoa x = At + B olevalla sijoituksella integraaliksi, jonka rajat ovat
f(x) dx
voidaan muuntaa muotoa x = At + B olevalla sijoituksella integraaliksi, jonka rajat ovat  ja
ja  . Suorita muuntaminen.
. Suorita muuntaminen.
Tehtävä 405
Osoita, että jos f on jatkuva funktio, niin
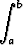 f(x) dx =
f(x) dx = 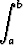 f(a + b - x) dx.
f(a + b - x) dx.
Tehtävä 406
Todista, että jos f jatkuva funktio, jolla on jaksona , niin
, niin
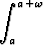 f(x) dx =
f(x) dx = 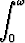 f(x) dx.
f(x) dx.
Tehtävä 407
Määritä
limn


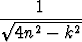 .
.
10.3 Osittaisintegrointi
Tehtävä 408
Laske osittaisintegroinnillaa) 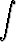 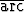 tan x dx, tan x dx, | b) 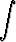 x2 cos x dx, x2 cos x dx, | c) 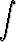 x3e-x dx, x3e-x dx, | |||||||||
d) 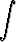 x cosh x dx, x cosh x dx, | e) 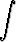 x ln 2x dx, x ln 2x dx, | f) 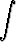 x x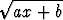 dx, dx, | |||||||||
g) 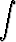 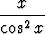 dx, dx, | h) 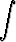 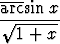 dx, dx, | i) 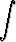 x x 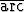 tan x dx. tan x dx. |
Tehtävä 409
Laske osittaisintegroinnilla
a) 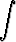 e
e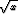 dx, b)
dx, b) 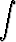 sin
sin 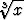 dx, c)
dx, c) 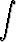
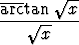 dx.
dx.
Tehtävä 410
Laske a)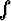 arsinh x dx, b)
arsinh x dx, b) 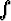
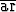 cosh x dx, c)
cosh x dx, c) 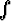 artanh x dx.
artanh x dx.
Tehtävä 411
Laske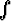 cos 2x dx a) osittaisintegroinnilla, b) soveltamalla sopivaa
trigonometrian kaavaa.
cos 2x dx a) osittaisintegroinnilla, b) soveltamalla sopivaa
trigonometrian kaavaa.
Tehtävä 412
Määritä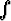 x
x ln x dx kaikilla arvoilla
ln x dx kaikilla arvoilla 

 .
.
Tehtävä 413
Muodosta osittaisintegroinnilla seuraavista integraaleista uusi integraali, joka ei ole laskettavissa alkeisfunktioiden avulla:
a) 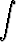
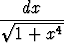 , b)
, b)  ex2
dx, c)
ex2
dx, c) 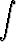
 dx, d)
dx, d) 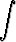
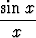 dx, e)
dx, e) 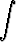
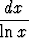 dx.
dx.
Tehtävä 414
Laske seuraavat määrätyt integraalit:a) 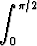 x cos 2x dx, x cos 2x dx, | b) 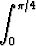 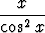 dx, dx, | c) 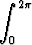 |x sin x| dx, |x sin x| dx, | |||||||||
d) 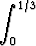 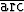 tan(3x) dx, tan(3x) dx, | e) 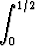 x x 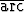 sin x dx, sin x dx, | f) 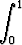 x2e3x dx, x2e3x dx, | |||||||||
g) 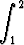 (x - 1)2 ln x dx, (x - 1)2 ln x dx, | h) 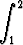 x ln 2x dx, x ln 2x dx, | i) 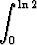 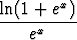 dx. dx. |
Tehtävä 415
Johda palautuskaava integraalille
In = 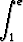 (ln x)n dx (n
(ln x)n dx (n 
 ).
).
Tehtävä 416
Johda palautuskaava integraalille
In = 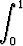 (1 - x2)n dx (n
(1 - x2)n dx (n 
 ).
).
Tehtävä 417
Johda osittaisintegroinnilla palautuskaava määrätylle integraalille
In = 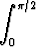 sin nx dx (n = 0, 1, 2, . . . ).
sin nx dx (n = 0, 1, 2, . . . ).
Tehtävä 418
Mitkä rajat saadaan luvulle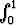 f(x) dx, kun tiedetään, että f ja sen
derivaatta ovat jatkuvia integroimisvälillä, f(1) = 1 ja |f'(x)| < ex2 integroimisvälillä?
f(x) dx, kun tiedetään, että f ja sen
derivaatta ovat jatkuvia integroimisvälillä, f(1) = 1 ja |f'(x)| < ex2 integroimisvälillä?
10.4 Rationaalifunktioiden integrointi; osamurtokehitelmä
Tehtävä 419
Integroi seuraavat rationaalifunktiot:a) 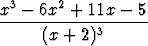 , , | b) 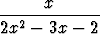 , , | c) 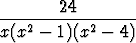 , , | |||||||||
d) 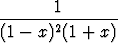 , , | e) 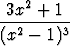 , , | f) 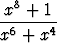 , , | |||||||||
g) 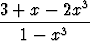 , , | h) 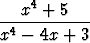 , , | i) 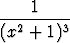 , , | |||||||||
j) 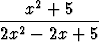 , , | k) 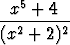 , , | l) 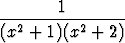 , , | |||||||||
m) 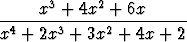 . . |
Tehtävä 420
Laske integraalit
a) 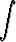
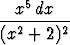 , b)
, b) 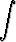
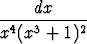 , c)
, c) 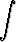
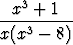 dx.
dx.
Tehtävä 421
Jaa polynomi x4 + 4 enintään toista astetta oleviin reaalisiin tekijöihin ja laske tätä hyväksi käyttäen integraali
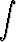
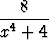 dx.
dx.
Tehtävä 422
Laske integraali
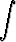
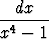 .
.
Tehtävä 423
Muodosta osamurtokehitelmä ja laske integraalifunktio lausekkeelle
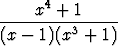 .
.
Tehtävä 424
Muodosta osamurtokehitelmä rationaalifunktiolle
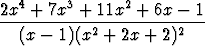
ja laske integraalifunktio.
Tehtävä 425
Laske integraali
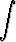
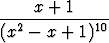 dx.
dx.
Tehtävä 426
Muodosta osamurtokehitelmä lausekkeelle
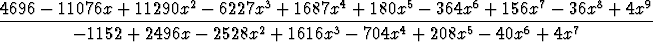 .
.
Lisää tämän jälkeen lausekkeen nimittäjään 1 ja muodosta osamurtokehitelmä uudelleen.
Tehtävä 427
Laske
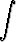
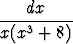
a) muodostamalla osamurtokehitelmä, b) suorittamalla ensin sopiva sijoitus.
Tehtävä 428
Olkoon a < b. Määritä se funktion
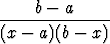
integraalifunktio, joka kohdassa 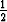 (a + b) saa arvon 0.
(a + b) saa arvon 0.
Tehtävä 429
Laske kaikilla arvoilla a
 integraali
integraali
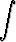
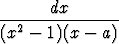 .
.
10.5 Esimerkkejä integroinnista
Tehtävä 430
Johda osittaisintegroinnilla palautuskaava integraalille
Cn = 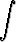 cos nx dx, n = 0, 1, 2, . . . .
cos nx dx, n = 0, 1, 2, . . . .
Laske myös C0 ja C1.
Tehtävä 431
Olkoon
Cn = 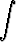 cos nx dx.
cos nx dx.
Johda kaavat
Cn = 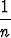 cos n-1x sin x + cos n-1x sin x + 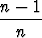 Cn-2, n Cn-2, n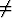 0, 0, | |||
Cn-2 = -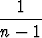 cos n-1x sin x + cos n-1x sin x + 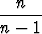 Cn, n Cn, n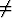 1. 1. |
Miten näiden avulla saadaan integraalit Cn, n 
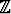 , lasketuiksi?
, lasketuiksi?
Tehtävä 432
Johda sijoitusta t = tan x käyttäen palautuskaava integraalille
In = 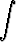 tan nx dx, n = 2, 3, 4, . . . .
tan nx dx, n = 2, 3, 4, . . . .
Laske erikseen I0 ja I1 sekä palautuskaavan avulla I5.
Tehtävä 433
Laske seuraavat integraalit:a) 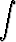 sin 7x dx, sin 7x dx, | b) 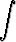 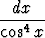 , , | c) 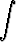 cos 6x dx, cos 6x dx, | |||||||||
d) 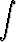 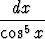 , , | e) 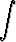 sin 24x cos 24x dx, sin 24x cos 24x dx, | f) 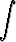 sin 23x sin 25x dx, sin 23x sin 25x dx, | |||||||||
g) 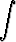 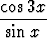 dx, dx, | h) 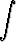 sin x sin 2x sin 3x dx, sin x sin 2x sin 3x dx, | i) 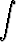 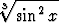 cos 3x dx, cos 3x dx, | |||||||||
j) 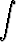 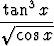 dx, dx, | k) 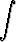 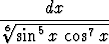 , , | l) 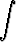 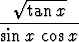 dx. dx. |
Tehtävä 434
Laske integraalita) 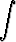 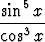 dx, dx, | b) 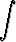 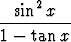 dx, dx, | c) 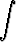 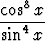 dx, dx, | |||||||||
d) 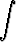 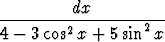 dx, dx, | e) 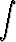 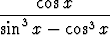 dx. dx. |
Tehtävä 435
Muunna integraali
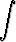
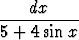
sijoituksella t = tan 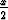 ja laske se. Piirrä integraalifunktion kuvaaja. Onko tämä jatkuva?
ja laske se. Piirrä integraalifunktion kuvaaja. Onko tämä jatkuva?
Tehtävä 436
Laske
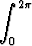
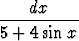 .
.
Tehtävä 437
Laske integraalit
a) 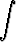
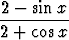 dx, b)
dx, b) 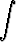
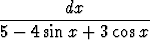 dx.
dx.
Tehtävä 438
Olkoon a > 0, b > 0. Laske
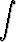
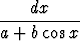 .
.
Tehtävä 439
Laske kaikilla arvoilla a

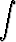
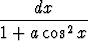 .
.
Tehtävä 440
Olkoon (a, b)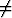 (0, 0). Laske
(0, 0). Laske
a) 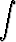
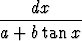 , b)
, b) 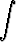
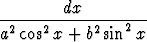 .
.
Tehtävä 441
Laske kaikilla arvoilla a, b

a) 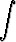 cos ax cos bx dx, b)
cos ax cos bx dx, b) 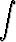 sin ax cos 2bx dx.
sin ax cos 2bx dx.
Tehtävä 442
Millä kokonaisluvun n arvoilla integraalit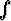 sinh nx dx ja
sinh nx dx ja 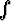 cosh nx dx
palautuvat polynomin integroimiseen? Millaista sijoitusta tällöin on käytettävä? Laske
sovellutuksena
cosh nx dx
palautuvat polynomin integroimiseen? Millaista sijoitusta tällöin on käytettävä? Laske
sovellutuksena
a) 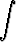 sinh 5x dx, b)
sinh 5x dx, b) 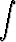 cosh 7x dx, c)
cosh 7x dx, c) 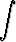
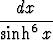 , d)
, d) 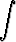
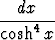 .
.
Tehtävä 443
Laske seuraavat integraalit:a) 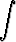 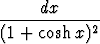 , , | b) 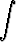 tanh 3x dx, tanh 3x dx, | c) 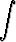 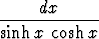 , , | d) 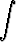 cosh 4x dx, cosh 4x dx, | ||||||||||||
e) 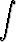 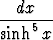 , , | f) 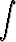 cosh 2x sinh 4x dx, cosh 2x sinh 4x dx, | g) 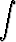 coth 2x dx, coth 2x dx, | h) 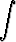 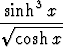 dx. dx. |
Tehtävä 444
Laske palauttamalla eksponenttifunktioon
a) (cosh x + sinh x)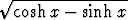 dx, b)
dx, b) 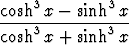 dx.
dx.
Tehtävä 445
Laske integraali
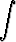
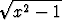 dx.
dx.
Tehtävä 446
Laske integraali
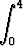
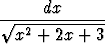 .
.
Anna vastaus logaritmifunktion avulla.
Tehtävä 447
Laske seuraavat integraalit:a) 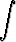 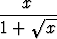 dx, dx, | b) 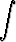 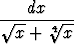 , , | c) 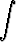 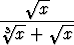 dx, dx, | |||||||||
d) 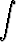 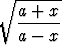 dx, dx, | e) 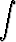 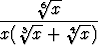 dx, dx, | f) 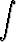 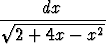 , , | |||||||||
g) 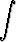 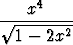 dx, dx, | h) 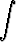 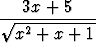 dx, dx, | i) 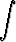 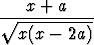 dx, dx, | |||||||||
j) 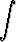 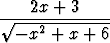 dx, dx, | k) 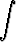 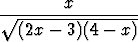 dx. dx. |
Tehtävä 448
Laske seuraavat määrätyt integraalit:a) 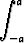 x2 x2 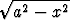 dx, dx, | b) 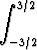 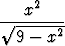 dx, dx, | c) 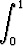 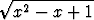 dx, dx, | |||||||||
d) 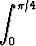 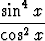 dx, dx, | e) 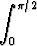 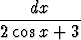 , , | f) 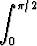 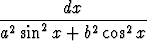 (ab (ab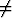 0). 0). |
Tehtävä 449
Sievennä funktio
f(x) = 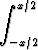
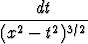 (x
(x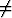 0)
0)
ja piirrä sen kuvaaja.
Tehtävä 450
Muotoa
I = 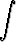
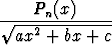 dx
dx
oleva integraali, missä Pn(x) on astetta n oleva polynomi, voidaan laskea kirjoittamalla
I = (A1 xn-1 + A2xn-2 + . . . + An)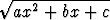 + An+1
+ An+1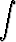
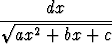 .
.
Osoita, että kertoimet Ak voidaan määrätä yksinomaan polynomien yhtäsuuruutta koskevasta ehdosta, joka saadaan asettamalla edellä olevien lausekkeiden derivaatat yhtä suuriksi. Sovella menettelyä seuraavien integraalien laskemiseen:
a) 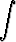
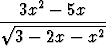 dx, b)
dx, b) 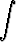
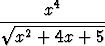 dx.
dx.
Tehtävä 451
Palauta annetuilla sijoituksilla integraalita) 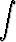 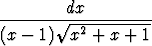 dx, x - 1 = dx, x - 1 = 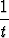 , , | |||
b) 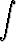 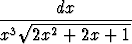 dx, x = dx, x = 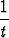 |
edellisessä tehtävässä käsiteltyyn muotoon ja laske ne.
Tehtävä 452
Palauta integraali
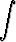
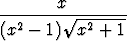 dx
dx
edellisessä tehtävässä käsiteltyyn tyyppiin muodostamalla ensin osamurtokehitelmä funktiolle x/(x2 - 1). Laske integraali.
Tehtävä 453
Laske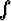 (ln x)n dx kaikille n
(ln x)n dx kaikille n 
 .
.
Tehtävä 454
Laske integraalita) 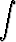 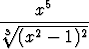 dx, dx, | b) 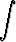 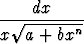 , , | c) 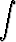 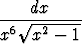 , , | |||||||||
d) 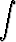 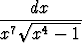 , , | e) 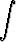 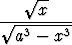 dx. dx. |
Tehtävä 455
Laske integraalita) 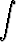 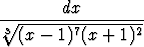 , , | b) 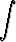 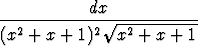 , , | ||||||
c) 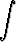 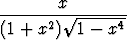 dx, dx, | d) 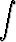 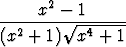 dx. dx. |
Tehtävä 456
Laske integraalit
a) 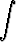 ln(
ln(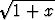 +
+ 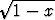 ) dx, b)
) dx, b) 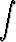
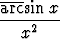 dx, c)
dx, c) 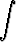 (1 + x2)2
(1 + x2)2 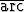 tan x dx.
tan x dx.
Tehtävä 457
Tutki, voidaanko seuraavat funktiot integroida alkeisfunktioiden avulla:
a) 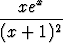 , b)
, b)  .
.
Tehtävä 458
Tutki, voidaanko seuraavat funktiot integroida alkeisfunktioiden avulla:
a) 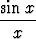 , b)
, b) 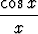 .
.