11 Määrätyn integraalin sovellutuksia
11.1 Pinta-ala ja tilavuus
Tehtävä 459
Laske sen rajoitetun alueen pinta-ala, jota reunustavat käyrät| a) y2 = 2x, x2 = 2y, | |||
b) y = 0, y = tan x, y = cot x (0 < x < 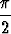 ), ), | |||
c) y = 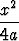 , y = , y = 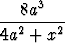 (a (a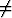 0), 0), | |||
| d) y = ln x, y = (ln x)2. |
Tehtävä 460
Laske sen alueen pinta-ala, joka on ympyrän r = a sisäpuolella, mutta Bernoulli’n lemniskaatan r2 = 2a2 cos 2 ulkopuolella.
ulkopuolella.
Tehtävä 461
Laske sen alueen pinta-ala, joka on ympyrän r = 6a cos sisäpuolella, mutta
kardioidin r = 2a(1 + cos
sisäpuolella, mutta
kardioidin r = 2a(1 + cos  ) ulkopuolella.
) ulkopuolella.
Tehtävä 462
Laske ympyröiden r = a cos ja r = b sin
ja r = b sin  rajoittamien alueiden
leikkauksen ala.
rajoittamien alueiden
leikkauksen ala.
Tehtävä 463
2a-sivuisen neliön keskipisteestä piirille piirrettyjä säteitä jatketaan janalla, jonka pituus on ka. Jatkettujen säteiden loppupisteet muodostavat umpinaisen käyrän. Laske tämän rajoittaman alueen pinta-ala.Tehtävä 464
Tason ympyrärenkaassa on kiinteä säde OAB, missä O on ympyrärenkaan keskipiste, A sisemmän ja B ulomman reunaympyrän kehällä. Säde OP kiertää keskipisteen O ympäri siten, että se alussa yhtyy säteeseen OA, lopussa säteeseen OB ja sen pituus on kiertokulman ensimmäisen asteen polynomi. Missä suhteessa saatu käyrä ja jana AB jakavat ympyrärenkaan pinta-alan?Tehtävä 465
Laske asteroidin x = a cos 3t, y = b sin 3t reunustaman alueen pinta-ala.Tehtävä 466
Laske sykloidinkaaren x = a(t - sin t), y = a(1 - cos t), t [0, 2
[0, 2 ], ja
x-akselin reunustaman alueen pinta-ala.
], ja
x-akselin reunustaman alueen pinta-ala.
Tehtävä 467
Laske tasokäyrän r(t) = (t2 - 1)(i + t j) muodostaman silmukan pinta-ala.Tehtävä 468
Laske lieriöiden x2 + y2 = R2, y2 + z2 = R2 ja z2 + x2 = R2 yhteisen osan tilavuus.Tehtävä 469
Laske sen kappaleen tilavuus, joka muodostuu seuraavan rajoitetun tasoalueen pyörähtäessä x-akselin ympäri:| a) käyrien y = x2 ja x = y2 reunustama alue, | |||
b) {(x, y) | x  ]0, ]0,  /4[, 0 < y < tan x}, /4[, 0 < y < tan x}, | |||
| c) asteroidin x = a cos 3t, y = b sin 3t reunustama alue, | |||
d) sykloidin kaaren x = a(t - sin t), y = a(1 - cos t), t  [0, 2 [0, 2 ], ja x-akselin reunustama alue, ], ja x-akselin reunustama alue, | |||
e) kardioidin r = a(1 + cos  ) reunustama alue. ) reunustama alue. |
Tehtävä 470
Akselin suhteen symmetrinen paraabelin segmentti, jonka kanta on b ja korkeus h, pyörähtää kannan ympäri. Laske muodostuvan kappaleen, ns. Cavalieri’n sitruunan tilavuus.Tehtävä 471
Tasokuvioa) {(x, y) | x  [0, 2 [0, 2 ], 0 < y < 1 - cos x}, ], 0 < y < 1 - cos x}, | |||
b) {(x, y) | x  [1, 3], 0 < y < (x - 1)(3 - x)} [1, 3], 0 < y < (x - 1)(3 - x)} |
pyörähtää y-akselin ympäri. Laske syntyvän kappaleen tilavuus.
Tehtävä 472
Olkoot a, b ja c positiivisia vakioita. Laske tilavuus kappaleelle{(x, y, z) | x > 0, y > 0, z > 0, z2 < a2 - bx - cy}.
Tehtävä 473
Kappaleen pohja on ympyrä, jonka säde on R. Jokainen kappaleen tasoleikkaus, joka on kohtisuorassa pohjaympyrän kiinteää halkaisijaa vastaan, on tasasivuinen kolmio. Laske kappaleen tilavuus. Hahmottele kuvio.Tehtävä 474
Tynnyrin korkeus on h, pohjaympyröiden säteet a ja keskikohdalta otetun poikkileikkausympyrän säde b. Laske tynnyrin tilavuus, kun sivulaudat kaartuvat paraabelin muotoisesti.Tehtävä 475
Kappaleen vaakasuorat tasoleikkaukset ovat neliöitä, joiden kärjet ovat R-säteisen pallon pinnalla. Laske kappaleen tilavuus. Määräytyykö kappale yksikäsitteisesti eo. ehdoista?Tehtävä 476
Jatkuvasti muuttuvan ympyrän keskipiste liikkuu täyden kierroksen pitkin ellipsiä b2 x2 + a2y2 = a2b2, sen taso on kohtisuorassa x-akselia vastaan ja se kulkee aina x-akselilla olevan pisteen kautta. Määritä liikkuvaa ympyrää peittävän kappaleen tilavuus.Tehtävä 477
Suoran ympyrälieriön pohjan säde on r ja korkeus h. Pohjan erään halkaisijan kautta asetetaan kaksi tasoa, jotka sivuavat toista pohjaympyrää. Laske lieriön ja tasojen rajoittaman kappaleen tilavuus.Tehtävä 478
Kahdella elliptisellä lieriöllä on yhteinen r-säteinen pohjaympyrä ja niiden toiset pohjaympyrät sivuavat toisiaan pisteessä, joka sijaitsee ensinmainitun pohjan keskipisteen kautta kulkevalla pohjatason normaalilla. Lieriöiden korkeus on h. Laske lieriöiden yhteisen osan tilavuus.11.2 Funktion keskiarvo
Tehtävä 479
Laske funktion
f(x) =  +
+ 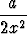
keskiarvo välillä [a, b]. Millä muuttujan arvolla 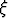 funktion arvo on ko. keskiarvo?
funktion arvo on ko. keskiarvo?
Tehtävä 480
Laske funktion
f(x) = 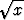 +
+ 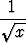
keskiarvo välillä [1, 4]. Millä muuttujan arvolla 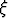 funktion arvo on ko. keskiarvo?
funktion arvo on ko. keskiarvo?
Tehtävä 481
Laske virran I(t) = I0 sin( t) ja jännitteen E(t) = E0 sin(
t) ja jännitteen E(t) = E0 sin( t -
t -  ) tulon
keskiarvo jakson pituisella välillä.
) tulon
keskiarvo jakson pituisella välillä.
Tehtävä 482
Laske funktioiden I1 sin( t +
t +  1) ja I2 sin(
1) ja I2 sin( t +
t +  2) summan neliön keskiarvo
jakson pituisella välillä.
2) summan neliön keskiarvo
jakson pituisella välillä.
11.3 Kaarenpituus ja pyörähdyspinnan ala
Tehtävä 483
Laske seuraavien käyränkaarien pituudet:a) y = 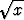 , x , x  [0, 1], [0, 1], | |||
b) y = ln x, x  [ [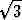 , , 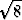 ], ], | |||
c) y = ln cos x, x  [0, [0, 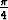 ], ], | |||
d) y = 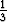 (3 - x) (3 - x)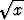 , x , x  [0, 3]. [0, 3]. |
Tehtävä 484
Laske pituus hyperbolisen spiraalin kaarelle r = 1/ ,
, 
 [
[ ,
,  ].
].
Tehtävä 485
Laske pituus logaritmisen spiraalin kaarelle r = e ,
, 
 [
[ ,
,  ].
].
Tehtävä 486
Laske asteroidin x = a cos 3t, y = a sin 3t koko pituus.Tehtävä 487
Laske sykloidin kaarenpituus: x(t) = a(t - sin t), y(t) = a(1 - cos t), t [0, 2
[0, 2 ].
].
Tehtävä 488
Johda ellipsin kehän pituudelle lauseke
a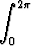
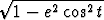 dt,
dt,
missä a on ellipsin ison akselin puolikas ja e eksentrisyys. Integraalia ei voida laskea alkeisfunktioiden avulla.
Tehtävä 489
Laske pituus ruuviviivankaarelle r(t) = a cos t i + a sin t j + bt k, t [0, 2
[0, 2 ].
].
Tehtävä 490
Laske väliä t [0, 1] vastaava kaarenpituus, kun käyrä on a) r(t) = t2 i + t3 j,
b) r(t) = t3 i + t2 j +
[0, 1] vastaava kaarenpituus, kun käyrä on a) r(t) = t2 i + t3 j,
b) r(t) = t3 i + t2 j +  t k.
t k.
Tehtävä 491
Johda kartion pinta-alan kaava pyörähdyspinnan alaa esittävästä integraalista.Tehtävä 492
Laske sen pinnan ala, joka syntyy, kun seuraava kaari pyörähtää x-akselin ympäri:a) y = x3, x  [0, 3], [0, 3], | |||
b) y = 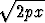 , x , x  [0, a]. [0, a]. |
Tehtävä 493
Ketjukäyrän y = a cosh , |x| < a, pyörähtäessä x-akselin ympäri syntyy
katenoidiksi kutsuttu pinta. Laske tämän ala. Hahmottele kuvio.
, |x| < a, pyörähtäessä x-akselin ympäri syntyy
katenoidiksi kutsuttu pinta. Laske tämän ala. Hahmottele kuvio.
Tehtävä 494
Asteroidi x = a cos 3t, y = a sin 3t pyörähtää x-akselin ympäri. Laske syntyvän pyörähdyspinnan ala.Tehtävä 495
Sykloidin kaari x(t) = a(t - sin t), y(t) = a(1 - cos t), t [0, 2
[0, 2 ], pyörähtää
x-akselin ympäri. Laske syntyvän pyörähdyspinnan ala.
], pyörähtää
x-akselin ympäri. Laske syntyvän pyörähdyspinnan ala.
Tehtävä 496
Laske ellipsoidin x2/a2 + y2/b2 + z2/b2 = 1 pinta-ala.Tehtävä 497
Laske ellipsin pyörähtäessä a) isoakselin, b) pikkuakselin ympäri muodostuvan ellipsoidin ala. Johda kummastakin pallon pinta-ala muodostamalla sopiva raja-arvo.11.4 Käyräteoriaa
Tehtävä 498
Määritä käyrän r(t) = t i + t2 j + t3 k kaarevuus ja kierevyys käyräparametrin t funktiona.Tehtävä 499
Määritä ruuviviivan r(t) = a cos t i + a sin t j + bt k jokaisessa pisteessä kolmikanta {t, n, b}, kaarevuus, kierevyys ja kaarevuuskeskipiste.Tehtävä 500
Etsi käyrälle
r(t) = et i + e-t j + 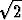 t k
t k
parametriesitys, jossa parametrina on kaarenpituus mitattuna jostakin kiinteästä pisteestä. Laske kaarenpituuden suhteen derivoimalla käyrän tangenttivektori, päänormaalivektori ja sivunormaalivektori sekä näiden avulla kaarevuus ja kierevyys. Laske erityisesti kaarevuus ja kierevyys arvoa t = 2 vastaavassa pisteessä.
Tehtävä 501
Laske sykloidin x(t) = a(t - sin t), y(t) = a(1 - cos t) kaarevuus parametrin t funktiona.Tehtävä 502
Olkoot a, b ja c vakiovektoreita. Laske käyränr(t) = t2 a + t b + c
kaarevuus ja kierevyys. Päättele, että kyseessä on tasokäyrä. Missä tasossa se sijaitsee?
Tehtävä 503
Määritä kolmikanta {t, n, b} ja oskuloiva taso parabolisten lieriöiden x2 = 2z ja y2 = 2z leikkauskäyrän jokaisessa pisteessä.Tehtävä 504
Määritä oskuloiva taso parabolisten lieriöiden x2 = 2az ja y2 = 2bz leikkauskäyrän jokaisessa pisteessä.Tehtävä 505
Laske käyränr(t) = (2t + 3) i + (3t - 1) j + t2 k
kierevyys ja päättele tästä, että kyseessä on tasokäyrä. Missä tasossa käyrä sijaitsee?
Tehtävä 506
Partikkelin ratakäyrä olkoon ellipsi r(t) = 2 cos t i + 3 sin t j, missä t on aika. Laske partikkelin nopeus- ja kiihtyvyysvektorit. Hajota kiihtyvyysvektori rata- ja normaalikomponentteihin. Määritä ratanopeuden suurin ja pienin arvo.Tehtävä 507
Kappaleen ratakäyrä avaruudessa onr(t) = (t2 - 1) i + (t3 - 3t2) j + 5t k,
missä t on aika. Laske partikkelin nopeusvektori, ratanopeus, kiihtyvyysvektori, ratakiihtyvyys ja normaalikiihtyvyys hetkellä t = 1. Mikä on tällöin radan kaarevuussäde?
Tehtävä 508
Kappale kulkee ellipsirataa, jonka toisessa polttopisteessä on origo. Nopeus määräytyy siten, että napakulma kasvaa vakionopeudella . Laske kappaleen
nopeusvektori ja ratanopeus ajan funktioina. Mikä on ratanopeus, jos ellipsiradan
eksentrisyys on = 0, ts. kyseessä on ympyrärata? Tiedoksi ellipsin napakoordinaattiyhtälö
. Laske kappaleen
nopeusvektori ja ratanopeus ajan funktioina. Mikä on ratanopeus, jos ellipsiradan
eksentrisyys on = 0, ts. kyseessä on ympyrärata? Tiedoksi ellipsin napakoordinaattiyhtälö
r = 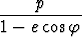 .
.
Tehtävä 509
Maapallon pinnalla kulkeva kappale lähtee liikkeelle päiväntasaajan ja nollameridiaanin leikkauspisteestä ja etenee siten, että sen leveysaste ja pituusaste kasvavat vakionopeudella . Laske kappaleen ratanopeus (= nopeusvektorin itseisarvo)
ajan funktiona. Piirrä tämän kuvaaja. (Valitse kuvaajassa
. Laske kappaleen ratanopeus (= nopeusvektorin itseisarvo)
ajan funktiona. Piirrä tämän kuvaaja. (Valitse kuvaajassa  = 1.) Minne kappale päätyy?
= 1.) Minne kappale päätyy?
Tehtävä 510
Tasokäyrä olkoon annettu muodossa y = y(x). Johda käyrän kaarevuudelle lauseke
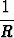 =
= ![|y''(x)|
------'--2-3/2-
[1 + y (x) ]](kuvat/ra1337x.gif) .
.
Tehtävä 511
Tasokäyrä olkoon annettu napakoordinaattimuodossa r = r( ). Johda
kaarevuudelle lauseke
). Johda
kaarevuudelle lauseke
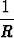 =
= 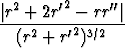 .
.
Tehtävä 512
Määritä kaarevuuden suurin arvo käyrällä a) y = x3, b) y2 = 2px, c) y = ln x. Määritä vastaavan kaarevuusympyrän keskipiste ja säde. Piirrä kuvio.Tehtävä 513
Määritä ellipsin akseleiden päätepisteisiin asetetut kaarevuusympyrät. Piirrä kuvio.Tehtävä 514
Lausu ellipsin b2x2 + a2y2 = a2b2 kaarevuus eksentrisen anomalian funktiona. Määritä kaarevuuden ääriarvot.Tehtävä 515
Määritä kaarevuus käyrälle
y = 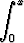 (1 + t) ln(1 + t) dt.
(1 + t) ln(1 + t) dt.
Tehtävä 516
Määritä a siten, että funktion
y = 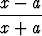
kuvaajan kaarevuussäde saa ääriarvon pisteessä (0, -1). Millainen ääriarvo on kyseessä?
Tehtävä 517
Laske kardioidin r = a(1 + cos ) kaarevuus napakulman
) kaarevuus napakulman  funktiona.
funktiona.
Tehtävä 518
Tutki logaritmisen spiraalin r = Cek kaarevuutta. Osoita, että käyrän
piste, kaarevuuskeskipiste ja origo muodostavat suorakulmaisen kolmion. Piirrä
kuvio.
kaarevuutta. Osoita, että käyrän
piste, kaarevuuskeskipiste ja origo muodostavat suorakulmaisen kolmion. Piirrä
kuvio.