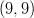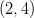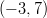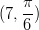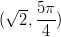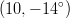Pikku-M: Koordinaatistot

Here be a line, if not the image is missing

Koordinaatistot

Geometriaa voidaan tarkastella Eukleideen tapaan puhtaana synteettisenä geometriana, jossa kuviot ovat suoraan tarkastelun kohteena. Toinen vaihtoehto on käyttää koordinaatteja, jolloin aluksi kiinnitetään jokin piste origoksi ja valitaan koordinaattiakselit. Tämän jälkeen pisteiden paikat ilmaistaan koordinaateilla, suorat ja käyrät yhtälöillä jne.

Koordinaatit on lähinnä ymmärrettävä luvuiksi, jotka jollakin tavoin yksikäsitteisesti täsmentävät pisteen paikan. Sekä tasoon että kolmiulotteiseen avaruuteen voidaan muodostaa erilaisia koordinaattijärjestelmiä.

Koordinaatiston ja koordinaattien käsite
Suorakulmainen koordinaatisto tasossa
Suorakulmainen koordinaatisto avaruudessa
Tason napakoordinaatisto
Pallokoordinaatit

Esimerkkejä

Esitetään karteesisen, eli suorakulmaisen, koordinaatiston piste 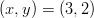$(x,y) = (3,2)$ napakoordinaattien avulla.

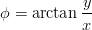Piste $(3,2 )$ sijaitsee koordinaatiston ensimmäisessä neljänneksessä, joten $y ϕ = arctan -- x$ .

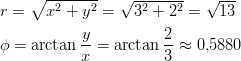
$∘ -------- √ ------- √ --- r = x2 + y2 = 32 + 22 = 13 ϕ = arctan y-= arctan 2-≈ 0,5880 x 3$

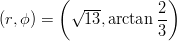Siis $( √ --- 2) (r,ϕ) = 13,arctan -- 3$ .
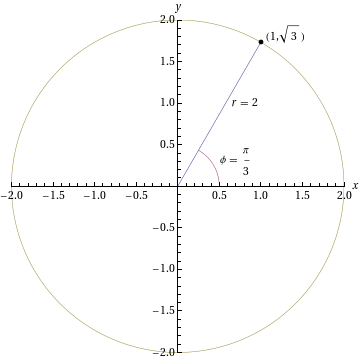
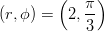Esitetään napakoordinaatiston piste $( π ) (r,ϕ ) = 2,3-$ karteesisessa koordinaatistossa.

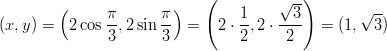
$( ) ( √ -) √ -- (x,y) = 2cos π,2 sin π- = 2 ⋅ 1,2 ⋅-3- = (1, 3) 3 3 2 2$
Esitetään piste 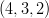$(4,3,2)$ pallokoordinaattien avulla.

$ϕ = arctan y-= arctan 3-≈ 0,644 x( 4 ) z ( 2 ) θ = arcsin ∘-------------- = arcsin √--2----2---2- x2 + y2 + z2 4 + 3 + 2 2 = arcsin √----≈ 0,381 ∘ ------29---- √------------ √ --- r = x2 + y2 + z2 = 42 + 32 + 22 = 29 ≈ 5,385$

Siis $( ) √ --- 3- -2--- (r,ϕ,θ) = 29, arctan4 , arcsin √ --- 29$ .

Harjoitustehtäviä

Esitä karteesisen koordinaatiston piste napakoordinaatteina.
1. $(9,9)$
2. $(2,4)$
3. $(− 3,7)$
Esitä napakoordinaatiston piste karteesisessa koordinaatistossa.
1. $(7, π-) 6$
2. $√ --5π ( 2,---) 4$
3. $(24, 3π-) 2$
4. $∘ (10,− 14 )$

Tehtävien vastaukset: