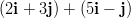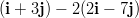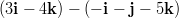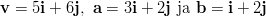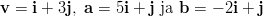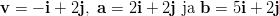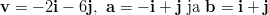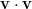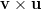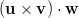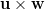Vektorit

Nimityksellä vektori voidaan tarkoittaa monia erilaisia asioita. Yksinkertaisimmillaan vektori on tason tai avaruuden olio, jolla on suuruus ja suunta. Tällaisia vektoreita voidaan havainnollistaa nuolilla.
Vektorien käyttökelpoisuus geometrian ja fysiikan työkaluna perustuu siihen, että vektoreilla voidaan laskea, ts. ne muodostavat algebran. Laskeminen tapahtuu joko suoraan vektorisymboleilla tai esittämällä vektorit koordinaatistossa.
 Vektorikäsite
Vektorikäsite Vektorien yhteenlasku ja skalaarilla kertominen
Vektorien yhteenlasku ja skalaarilla kertominen Vektorit koordinaatistossa
Vektorit koordinaatistossa
Tehokkaimmat vektorialgebran työkalut ovat skalaaritulo sekä tasossa että avaruudessa ja vektoritulo avaruudessa. Näiden avulla voidaan mm. johtaa melko yksinkertaisesti monia analyyttisen geometrian ja pallonpintageometrian kaavoja.
 Skalaaritulo
Skalaaritulo Vektorin komponentti
Vektorin komponentti Vektoritulo
Vektoritulo Vektoritulon laskeminen
Vektoritulon laskeminen

Esimerkkejä
- Lasketaan yhteen vektorit
 ja
ja 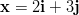 .
.
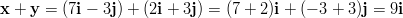
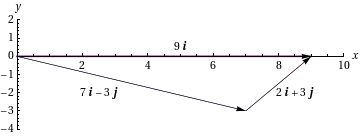
- Jaetaan vektori
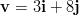 vektoreiden
vektoreiden 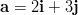 ja
ja 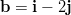 suuntaisiin komponentteihin.
suuntaisiin komponentteihin.
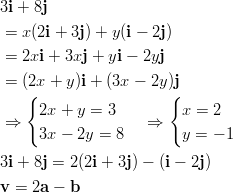

- Lasketaan vektoreiden
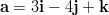 ja
ja 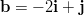 välinen kulma
käyttäen pistetulon kaavaa
välinen kulma
käyttäen pistetulon kaavaa 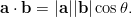
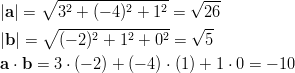
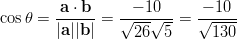
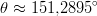
- Vektoria
 merkitään usein myös pisteellä
merkitään usein myös pisteellä  , kun voidaan
olettaa kantavektoiden
, kun voidaan
olettaa kantavektoiden 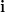 ja
ja  olevan tunnettuja. Esimerkiksi
skalaarikoordinaatiston vektoria
olevan tunnettuja. Esimerkiksi
skalaarikoordinaatiston vektoria 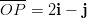 voidaan lyhemmin
merkitä
voidaan lyhemmin
merkitä  ja vektoreiden
ja vektoreiden 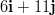 ja
ja 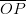 summa saadaan
seuraavasti:
summa saadaan
seuraavasti: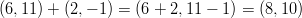
- Ristitulo vektoreista
 ja
ja 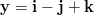 on vektori, joka on
kohtisuorassa kumpaakin tulon tekijävektoria vastaan. (Sen suunta
määräytyy ns. oikean käden säännön nojalla.)
on vektori, joka on
kohtisuorassa kumpaakin tulon tekijävektoria vastaan. (Sen suunta
määräytyy ns. oikean käden säännön nojalla.)


Harjoitustehtäviä
- Puolisuunnikkaan
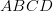 sivu
sivu  on kaksi kertaa niin pitkä kuin sen
kanssa yhdensuuntainen sivu
on kaksi kertaa niin pitkä kuin sen
kanssa yhdensuuntainen sivu  . Ilmaise vektorien
. Ilmaise vektorien  ja
ja
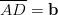 avulla
avulla
- sivuvektori
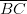
- lävistäjävektori
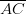 .
.
- sivuvektori
- Millä vakion
 arvoilla vektoreille
arvoilla vektoreille 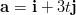 ja
ja 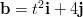 pätee,
että
pätee,
että
-
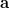 ja
ja 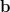 yhdensuuntaisia
yhdensuuntaisia
-
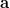 :n ja
:n ja  :n erotus ja summa ovat kohtisuorassa toisiaan
vasten.
:n erotus ja summa ovat kohtisuorassa toisiaan
vasten.
-
- Laske
-
- Jaa vektori
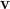 komponentteihin
komponentteihin  ja
ja 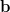 , kun
, kun
-
- Laske, kun
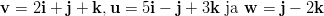 .
.
-
- Mistä xy-tason pisteestä pisteisiin
 ,
, 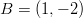 ,
,
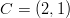 ,
,  ja
ja 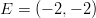 piirrettyjen vektoreiden
summa on nollavektori?
piirrettyjen vektoreiden
summa on nollavektori?
Tehtävien vastaukset: