Esimerkkejä normaaleista aliryhmistä ja tekijäryhmistä

Esimerkki. Säännöllisten (n×n)-matriisien joukko GL_n() = {A M_n×n() | det(A)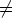0} on ryhmä matriisien kertolaskun suhteen. Joukon GL_n() osajoukko SL_n() = {A GL_n() | det(A) = 1} muodostaa tämän aliryhmän. Näytetään, että tämä aliryhmä on normaali.

Kaikilla A GL_n() ja B SL_n() on

joten ABA^-1 SL _n(). Aliryhmien normaalisuuskriteerin mukaan SL_n() on normaali aliryhmä matriisien kertolaskun suhteen.

Esimerkki. Merkitään ^* = \{0} ja H = < -1 > = {±1}. Silloin (H, ^. ) on ryhmän (^*, ^. ) aliryhmä. Koska (^*, ^. ) on Abelin ryhmä, on (H, ^. ) normaali. Ryhmän (^*, ^. ) tekijäryhmä aliryhmän (H, ^. ) suhteen on

varustettuna binäärioperaatiolla aH ^. bH = abH kaikilla positiivisilla reaaliluvuilla a ja b.

Esimerkki. Abelin ryhmän (, +) normaali aliryhmä on (< m >, +) = (_m, +), kun m > 1. Ryhmän (, +) tekijäryhmän tämän aliryhmän suhteen muodostaa

kun binäärioperaationa on (k + m) + (h + m) = (k + h) + m. Toisin merkittynä:

ja binäärioperaationa on + = . Siis (/m, +) on jäännösluokkaryhmä modulo m eli /m = _m .

Linkit:
Normaali aliryhmä
Tekijäryhmä
Esimerkkejä aliryhmistä
Säännöllinen matriisi