Sanna Ranto, LUKUTEORIA JA ALGEBRA
Versio 1, 1.11.2003 		RENGAS
 

Esimerkkejä rengashomomorfismeista

Esimerkki. Olkoon (R, +, . ) rengas. Identiteettikuvaus id R : (R, +, . ) --> (R, +, . ), missä kaikilla a (- R on idR(a) = a, on rengasisomorfismi.

Nollakuvaus f(a) = 0R kaikilla a (- R ei ole homomorfismi, koska se ei toteuta ehtoa RH3.

Esimerkki. Kuvaus f : (R[x], +, . ) --> (R, +, . ), missä f(a 0 + a1x + ... + anxn) = a 0, on rengashomomorfismi. Nimittäin, jos a0 + a1x + ... + anxn,b 0 + b1x + ... + bmxm (- R[x] (voidaan olettaa, että m > n), niin

f(a0+...+anxn+b0+...+bmxm) = f(a0+b0+(a1+b1)x+...+(an+bn)xn+bn+1xn+1+...+bmxm) = a + b = f (a + a x + ...+ a xn) + f(b + b x + ...+ b xm). 0 0 0 1 n 0 1 m
Lisäksi
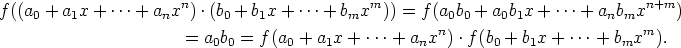f((a0+a1x+ ...+ anxn) .(b0 + b1x + ...+ bmxm)) = f (a0b0 + a0b1x + ...+ anbmxn+m) n m = a0b0 = f (a0 + a1x + ...+ anx ) .f(b0 + b1x + ...+ bmx ).
Renkaan (R[x], +, . ) ykkösalkio on luku 1. Koska f(1) = 1, niin myös viimeinen rengashomomorfismin ehto toteutuu.

Tämän rengashomomorfismin ydin ker(f) on

ker(f) = {p(x) (- R[x] |f(p(x)) = 0R = 0} = {p(x) (- R[x] |polynomin p(x) vakiotermi on 0}.
Rengashomomorfismin kuva Im (f) on reaalilukujen joukko R. Kyseessä on siis epimorfismi.

Renkaiden homomorfialauseen mukaan rengashomomorfismi f indusoi rengasisomorfismin

F : (R[x]/ ker(f),+, .) --> (R,+, .),

missä F (a0 + a1x + 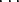... + anxn + ker(f)) = F(a 0 + ker(f)) = f(a0) = a0.

Esimerkki. Näytetään, että kuvaus f : (C, +, . ) --> (C, +, . ), missä f(x + iy) = x - iy, on rengasautomorfismi. Kuvaus f on homomorfismi sillä kaikilla x1 + iy1,x2 + iy2 (- C on

f(x1+iy1 + x2 + iy2) = f(x1 + x2 + i(y1 + y2)) = x1 + x2 - i(y1 + y2) = x1 - iy1 + x2- iy2 = f (x1 + iy1) + f(x2 + iy2)
ja
f((x+iy)(x + iy )) = f(x x - y y + i(x y + y x )) = x x - y y - i(x y + y x ) 112 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 = (x1 - iy1)(x2 - iy2) = f(x1 + iy2)f (x2 + iy2).
Renkaan C ykkösalkio on 1. Koska f(1) = 1, toteutuvat kaikki rengashomomorfismin ehdot.

Homomorfismi on injektio, sillä ker(f) = {0}. Selvästi homomorfismi on myös surjektio, joten se on bijektio ja näin ollen automorfismi.

Linkit:
Esimerkkejä alirenkaista
Renkaiden homomorfia
Rengashomomorfismin ydin ja kuva
Renkaiden homomorfialause