Polynomien jaollisuus

Oletetaan nyt, että polynomien kertoimet kuuluvat kuntaan (K, +, ^. ). Ensimmäiseksi tietysti tulee mieleen, onko polynomirengas (K[x], +, ^. ) kunta. Vastaus tähän on kielteinen. Nimittäin polynomilla f(x) K[x] on käänteisalkio vain ja ainoastaan jos f(x) on nollapolynomista eroava vakiopolynomi. Tämä nähdään käyttämällä sivun Polynomin aste lausetta. Oletetaan, että g(x) K[x] on polynomin f(x) käänteialkio. Silloin f(x)g(x) = 1_K, joten edellä mainitun lauseen mukaan 0 = deg(f(x)g(x)) = deg f(x) + deg g(x). Koska polynomin aste on aina vähintään nolla tai se on -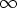, niin saadusta yhtälöstä seuraa, että deg f(x) = deg g(x) = 0 eli molemmat polynomit ovat nollapolynomista eroavia vakiopolynomeja.

Sivun Polynomin aste lauseen mukaan polynomirengas (K[x], +, ^. ) on kokonaisalue, mutta ei siis kunta. Tämän renkaan rakenne on siis sama kuin kokonaislukujen renkaankin (, +, ^. ); se on kokonaisalue, mutta ei kunta. Polynomeille yli kunnan K saadaankin samanlainen jaollisuusteoria kuin kokonaisluvuille.

Määritelmä. Olkoon (K[x], +, ^. ) polynomirengas yli kunnan K ja a(x),b(x) K[x]. Jos on olemassa sellainen polynomi c(x) K[x], että a(x) = b(x)c(x), niin sanotaan, että a(x) on jaollinen polynomilla b(x). Tätä merkitään b(x) | a(x). Voidaan sanoa myös b(x) jakaa polynomin a(x), b(x) on polynomin a(x) tekijä, tai a(x) on polynomin b(x) monikerta.

Polynomien yli kunnan K jaollisuusrelaatiolla on useita samoja ominaisuuksia kuin kokonaisluvuilla. Esimerkiksi aina a(x) | a(x) ja

Eräät ominaisuudet ovat hieman toisenlaisia. Esimerkiksi

Nimittäin oletuksesta seuraa, että joillain polynomeilla c(x) ja d(x) K[x] on a(x) = c(x)b(x) ja b(x) = d(x)a(x), joten a(x) = c(x)d(x)a(x). Koska K[x] on kokonaisalue, siinä on voimassa supistamissääntö, joten saadaan 1_K = c(x)d(x). Kuten sivun alussa huomattiin tästä seuraa, että c(x), d(x) K \{0_K}. Tästä puolestaan seuraa väite.

Linkit:
Polynomirengas
Polynomin aste
Jaollisuus ja alkuluvut
Esimerkkejä polynomirenkaista
Ryhmän perusominaisuuksia