Polynomien jakoalgoritmi

Tutkittaessa polynomien yli kunnan (K, +, ^. ) jaollisuutta voidaan käyttää samanlaista jakoalgoritmia (jakokulmalaskua) kuin kokonaisluvuilla. Vertaa seuraavaa lausetta sivun Jakoalgoritmi lauseeseen.

Lause. Olkoon (K[x], +, ^. ) polynomirengas yli kunnan (K, +, ^. ). Jos a(x),b(x) K[x] ja b(x)0_K, niin on olemassa sellaiset yksikäsitteiset polynomit q(x) ja r(x) K[x], että

Todistus. Olkoon S = {a(x) - k(x)b(x) | k(x) K[x]}. Valitaan joukosta S polynomi

jonka aste on pienin mahdollinen. Jos r(x) = 0_K, niin deg r(x) = -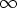 < deg b(x) ja lauseen väite on voimassa.

Oletetaan, että r(x) ei ole nollapolynomi ja deg r(x) = n. Oletetaan lisäksi, että deg b(x) = m. Pitää siis näyttää, että n < m. Olkoon polynomin r(x) johtava kerroin r_n ja polynomin b(x) johtava kerroin b_m. Tehdään vastaoletus, että n > m. Koska b_m K \{0_K}, on olemassa käänteisalkio b K. Tämän huomion ja vastaoletuksen nojalla voidaan muodostaa polynomi

Polynomi s(x) kuuluu joukkoon S ja sen n:nnen asteen termin kerroin on

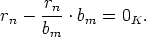
Siis s(x) on pienempää astetta kuin polynomi r(x), mikä on ristiriita polynomin r(x) valinnan kanssa. Täten n < m.

Vielä pitää osoittaa polynomien q(x) ja r(x) yksikäsitteisyys. Oletetaan, että on olemassa myös polynomit q'(x) ja r'(x), joilla a(x) = q'(x)b(x) + r'(x) ja deg r'(x) < deg b(x). Silloin

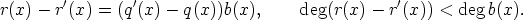
Toisaalta sivun Polynomin aste lauseen mukaan deg(r(x) -r'(x)) = deg(q'(x) -q(x)) + deg b(x). Täten välttämättä q'(x) - q(x) = 0_K ja tästä seuraa, että r(x) - r'(x) = 0_Kb(x) = 0_K. Siis q(x) = q'(x) ja r(x) = r'(x).

Linkit:
Polynomien jaollisuus
Jakoalgoritmi
Polynomin aste
Esimerkkejä polynomirenkaista