![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät
Sisällön pääryhmät  Luvut
Luvut  Alkutekijät [ 1 2 3 4
]
Alkutekijät [ 1 2 3 4
]
ESITIEDOT:
KATSO MYÖS:
![[#]](kuvat/msam10-c-4.gif) Kansisivu Kansisivu
![[#]](kuvat/msam10-c-4.gif) Sisältö Sisältö
![[#]](kuvat/msam10-c-4.gif) Hakemisto Hakemisto |
![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät Sisällön pääryhmät  Luvut Luvut  Alkutekijät [ 1 2 3 4
] Alkutekijät [ 1 2 3 4
]
ESITIEDOT: KATSO MYÖS: |
|
Alkuluvuiksi sanotaan jaottomia luonnollisia lukuja ( 1):
1):
| 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, | ||||
| 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, | ||||
| 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, | ||||
| 193, 197, 199, 211, 223, 227, 229, 233, 239, 241, 251, ... . |
123456789 = 32 . 3607 . 3803, 90642552 = 23 . 3 . 74 . 112 . 13.
Luonnollisen luvun n jakaminen alkutekijöihin voidaan alkeellisesti tehdä
kokeilemalla: Tutkitaan, onko luku jaollinen alkuluvuilla, jotka ovat < 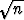 . Tällöin
on apua seuraavassa esitettävistä jaollisuussäännöistä.
. Tällöin
on apua seuraavassa esitettävistä jaollisuussäännöistä.
![[#]](kuvat/msam10-c-4.gif) luonnollinen luku luonnollinen luku |
Kivelä,  niinkuin matematiikka, versio 1.12
niinkuin matematiikka, versio 1.12