![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät
Sisällön pääryhmät  Diskreettiä matematiikkaa
Diskreettiä matematiikkaa  Logiikka [ 1 2
3 4 5 ]
Logiikka [ 1 2
3 4 5 ]
ESITIEDOT:
KATSO MYÖS:
![[#]](kuvat/msam10-c-4.gif) Kansisivu Kansisivu
![[#]](kuvat/msam10-c-4.gif) Sisältö Sisältö
![[#]](kuvat/msam10-c-4.gif) Hakemisto Hakemisto |
![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät Sisällön pääryhmät  Diskreettiä matematiikkaa Diskreettiä matematiikkaa  Logiikka [ 1 2
3 4 5 ] Logiikka [ 1 2
3 4 5 ]
ESITIEDOT: KATSO MYÖS: |
|
Propositioista p ja q voidaan johtaa uusia propositioita käyttämällä seuraavia loogisia operaattoreita eli konnektiiveja:
| konjunktio: | p 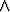 q q | ’p ja q’, |
| disjunktio: | p 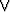 q q | ’p tai q’, |
| negaatio: | ¬p | ’ei p’, |
| implikaatio: | p 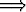 q q | ’p:stä seuraa q’, ’jos p niin q’, |
| ekvivalenssi: | p 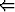 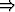 q q | ’p ja q ovat yhtäpitäviä’, |
| ’p jos ja vain jos q’. |
Näiden merkitys on pääosin luonnollisen logiikan mukainen. Täsmällinen merkitys ilmenee seuraavasta totuusarvotaulusta, missä loogisen operaattorin avulla saadun proposition totuusarvo on määritelty kaikkia propositioiden p ja q totuusarvoja vastaten (1 = tosi, 0 = epätosi).
| p | q | ¬p | p 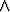 q q | p 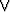 q q | p 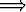 q q | p 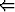 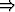 q q |
| 1 | 1 | 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 | 1 | 1 | 0 |
| 0 | 0 | 1 | 0 | 0 | 1 | 1 |
Erityisesti on syytä huomata disjunktion merkitys: p 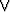 q tarkoittaa siis ’p tai q tai
molemmat’. Kyseessä on siten ns. ’ei-poissulkeva tai’. Luonnollisen logiikan
kannalta ei myöskään liene itsestään selvää, että p
q tarkoittaa siis ’p tai q tai
molemmat’. Kyseessä on siten ns. ’ei-poissulkeva tai’. Luonnollisen logiikan
kannalta ei myöskään liene itsestään selvää, että p 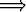 q on tosi propositiosta q
riippumatta, jos p on epätosi. Kyseessä onkin tarkoituksenmukaisuussyistä tehty
määrittely; tavoitteena on toimiva kalkyyli.
q on tosi propositiosta q
riippumatta, jos p on epätosi. Kyseessä onkin tarkoituksenmukaisuussyistä tehty
määrittely; tavoitteena on toimiva kalkyyli.
Eo. määrittelyissä p ja q ovat atomipropositioita; konnektiivien avulla muodostetut ovat johdettuja propositioita. Mistä tahansa propositioista voidaan muodostaa uusia propositioita yhdistelemällä niitä konnektiivien avulla.
Jos johdettu propositio on tosi riippumatta sen atomipropositioiden totuusarvoista, sitä sanotaan tautologiaksi. Esimerkki seuraavassa.
Kivelä,  niinkuin matematiikka, versio 1.12
niinkuin matematiikka, versio 1.12