![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät
Sisällön pääryhmät  Diskreettiä matematiikkaa
Diskreettiä matematiikkaa  Logiikka [ 1 2
3 4 5 ]
Logiikka [ 1 2
3 4 5 ]
ESITIEDOT:
KATSO MYÖS:
![[#]](kuvat/msam10-c-4.gif) Kansisivu Kansisivu
![[#]](kuvat/msam10-c-4.gif) Sisältö Sisältö
![[#]](kuvat/msam10-c-4.gif) Hakemisto Hakemisto |
![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät Sisällön pääryhmät  Diskreettiä matematiikkaa Diskreettiä matematiikkaa  Logiikka [ 1 2
3 4 5 ] Logiikka [ 1 2
3 4 5 ]
ESITIEDOT: KATSO MYÖS: |
|
Olkoon tarkasteltavana johdettu propositio r:
(p 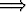 q)
q) 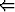
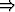 (¬q
(¬q 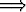 ¬p).
¬p).
Tämän totuusarvo voidaan selvittää muodostamalla totuusarvotaulu, missä p ja q saavat kaikki mahdolliset totuusarvot:
| p | q | ¬p | ¬q | p 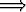 q q | ¬q  ¬p ¬p | r |
| 1 | 1 | 0 | 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 0 | 1 | 1 | 1 |
| 0 | 0 | 1 | 1 | 1 | 1 | 1 |
Osoittautuu siis, että propositio r on aina tosi, ts. se on tautologia. Tämä
merkitsee, että propositiot p 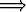 q ja ¬q
q ja ¬q 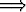 ¬p ovat joko molemmat tosia tai
molemmat epätosia.
¬p ovat joko molemmat tosia tai
molemmat epätosia.
Kyseessä on itse asiassa matematiikassa paljon käytetyn epäsuoran todistamisen periaate. Luonnollista logiikkaa käyttäen tämän voi esittää seuraavasti:
Jos on osoitettava, että lausumasta p seuraa lausuma q, mutta tämän päättely
osoittautuu vaikeaksi, voidaankin tarkastella, mitä tapahtuu, jos q ei ole voimassa.
Tutkitaan siis, mitä seuraa lausumasta ¬q, ns. vastaoletuksesta eli antiteesista. Jos
tällöin voidaan osoittaa, että ¬p on voimassa, päädytään ristiriitaan, koska
alkuperäisessä tehtävässä p on tosi. Lausuma ¬q ei siis voi olla tosi, ts. q on
tosi. Alkuperäisen tehtävän p 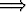 q sijasta tässä siis todistetaankin, että
¬q
q sijasta tässä siis todistetaankin, että
¬q 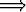 ¬p.
¬p.
Esimerkkinä epäsuoran todistuksen käytöstä olkoon seuraavan lauseen todistaminen:
Ei ole olemassa suurinta alkulukua. Tämä lause on propositio q; propositio p muodostuu kaikista tunnetuista luonnollisten lukujen ominaisuuksista. Propositio ¬q on tällöin ’on olemassa suurin alkuluku’.
Olkoon siis suurin alkuluku olemassa ja tämä olkoon n. Tällöin alkulukuja on äärellinen määrä; nämä ovat 2, 3, 5, 7, ..., n. Olkoon m = (2 . 3 . 5 . 7 . ... . n) + 1. Jos tämä jaetaan millä tahansa alkuluvuista 2, 3, 5, 7, ..., n, saadaan jakojäännökseksi 1. Koska jako ei mene tasan, on m alkuluku, jolloin se on pienempi tai yhtä suuri kuin suurin alkuluku n; siis m < n. Selvästi on kuitenkin m > n, jolloin on syntynyt ristiriita luonnollisten lukujen suuruusjärjestykseen nähden.
![[#]](kuvat/msam10-c-4.gif) alkuluku alkuluku![[#]](kuvat/msam10-c-4.gif) luonnollinen luku luonnollinen luku |
Kivelä,  niinkuin matematiikka, versio 1.12
niinkuin matematiikka, versio 1.12