![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät
Sisällön pääryhmät  Diskreettiä matematiikkaa
Diskreettiä matematiikkaa  Logiikka [ 1 2
3 4 5 ]
Logiikka [ 1 2
3 4 5 ]
ESITIEDOT:
KATSO MYÖS:
![[#]](kuvat/msam10-c-4.gif) Kansisivu Kansisivu
![[#]](kuvat/msam10-c-4.gif) Sisältö Sisältö
![[#]](kuvat/msam10-c-4.gif) Hakemisto Hakemisto |
![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät Sisällön pääryhmät  Diskreettiä matematiikkaa Diskreettiä matematiikkaa  Logiikka [ 1 2
3 4 5 ] Logiikka [ 1 2
3 4 5 ]
ESITIEDOT: KATSO MYÖS: |
|
Muotoa ’x > 5’ tai ’x ja y ovat naimisissa’ olevat lausumat eivät ole propositioita, koska niiden totuusarvo riippuu siitä, mitä muuttujien x ja y paikalle sijoitetaan. Tällaisia vapaista muuttujista riippuvia lausumia kutsutaan predikaateiksi ja niitä merkitään funktioiden tapaan: p(x), m(x, y).
Kun muuttuja(t) sidotaan, esimerkiksi niille annetaan arvot jostakin perusjoukosta,
predikaatit muuttuvat propositioiksi. Edellisen esimerkin tapauksessa luonnollinen
perusjoukko on reaalilukujoukko  ja asettamalla x =
ja asettamalla x =  saadaan epätosi
propositio
saadaan epätosi
propositio  > 5. Jälkimmäisessä esimerkissä muuttujan x luonnollinen
perusjoukko muodostuu kaikista miehistä, muuttujan y kaikista naisista, jolloin
esimerkiksi ’(tietty) Pekka ja (tietty) Maija ovat naimisissa’ on propositio, jonka
totuusarvo on mahdollista selvittää.
> 5. Jälkimmäisessä esimerkissä muuttujan x luonnollinen
perusjoukko muodostuu kaikista miehistä, muuttujan y kaikista naisista, jolloin
esimerkiksi ’(tietty) Pekka ja (tietty) Maija ovat naimisissa’ on propositio, jonka
totuusarvo on mahdollista selvittää.
Muuttujat voidaan sitoa myös kvanttoreilla, joista tärkeimmät ovat seuraavat:
| kaikilla-kvanttori: | 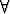 x p(x) x p(x) | ’kaikilla x on ominaisuus p(x)’, |
| on olemassa -kvanttori: | 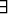 x p(x) x p(x) | ’on olemassa x, jolla |
| on ominaisuus p(x)’. |
Esimerkiksi sitomalla predikaatti |x| > 0 kaikilla-kvanttorilla (perusjoukkona
reaaliluvut) saadaan propositio 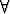 x (|x| > 0), joka on tosi.
x (|x| > 0), joka on tosi.
Sitomalla predikaatti x2 < 0 on olemassa -kvanttorilla (perusjoukkona reaaliluvut)
saadaan epätosi propositio 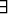 x (x2 < 0). Jos perusjoukkona sen sijaan ovat
kompleksiluvut, saadaan tosi propositio.
x (x2 < 0). Jos perusjoukkona sen sijaan ovat
kompleksiluvut, saadaan tosi propositio.
Jos predikaatissa on useampia muuttujia, nämä on kaikki sidottava. Esimerkiksi
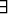 x
x 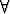 y m(x, y) on epätosi, kun m(x, y) on predikaatti ’x ja y ovat naimisissa’.
y m(x, y) on epätosi, kun m(x, y) on predikaatti ’x ja y ovat naimisissa’.
Predikaateille voidaan muodostaa laskusääntöjä. Luonnollisen logiikan pohjalta esimerkiksi seuraavat ovat ilmeisiä:
¬ 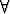 x p(x) x p(x) 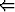 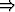 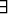 x ¬p(x), x ¬p(x), | |||
¬ 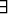 x p(x) x p(x) 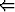 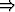 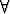 x ¬p(x), x ¬p(x), | |||
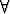 x [p(x) x [p(x) 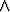 q(x)] q(x)] 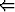 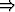 [ [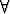 x p(x) x p(x) 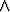 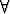 x q(x)], x q(x)], | |||
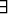 x [p(x) x [p(x) 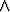 q(x)] q(x)] 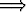 [ [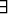 x p(x) x p(x) 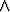 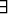 x q(x)]. x q(x)]. |
![[#]](kuvat/msam10-c-4.gif) funktio funktio![[#]](kuvat/msam10-c-4.gif) itseisarvo (reaaliluvun) itseisarvo (reaaliluvun)![[#]](kuvat/msam10-c-4.gif) reaaliluku reaaliluku![[#]](kuvat/msam10-c-4.gif) kompleksiluku kompleksiluku |
Kivelä,  niinkuin matematiikka, versio 1.12
niinkuin matematiikka, versio 1.12