![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät
Sisällön pääryhmät  Integraali
Integraali  Massakeskipiste [ 1 2
]
Massakeskipiste [ 1 2
]
ESITIEDOT:
![[#]](kuvat/msam10-c-4.gif) keskiarvo,
keskiarvo, ![[#]](kuvat/msam10-c-4.gif) määrätty integraali
määrätty integraali
KATSO MYÖS:
![[#]](kuvat/msam10-c-4.gif) integroimistekniikkaa,
integroimistekniikkaa, ![[#]](kuvat/msam10-c-4.gif) hitausmomentti
hitausmomentti
![[#]](kuvat/msam10-c-4.gif) Kansisivu Kansisivu
![[#]](kuvat/msam10-c-4.gif) Sisältö Sisältö
![[#]](kuvat/msam10-c-4.gif) Hakemisto Hakemisto |
![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät Sisällön pääryhmät  Integraali Integraali  Massakeskipiste [ 1 2
] Massakeskipiste [ 1 2
]
ESITIEDOT: ![[#]](kuvat/msam10-c-4.gif) keskiarvo, keskiarvo, ![[#]](kuvat/msam10-c-4.gif) määrätty integraali määrätty integraali
KATSO MYÖS: ![[#]](kuvat/msam10-c-4.gif) integroimistekniikkaa, integroimistekniikkaa, ![[#]](kuvat/msam10-c-4.gif) hitausmomentti hitausmomentti
|
|
Olkoon tarkasteltavana puoliympyrän muotoinen homogeeninen levy, ts. levy jonka massatiheys on vakio. Geometrinen keskiö ja massakeskipiste ovat tällöin sama asia. Lasketaan tämän koordinaatit.
Sijoitetaan koordinaatisto siten, että origo yhtyy puoliympyrän keskipisteeseen ja levy sijaitsee x-akselin yläpuolella. Tällöin levyn reunoina ovat x-akseli ja ympyrän x2 + y2 = R2 kaari, missä y > 0.
Symmetriasyistä keskiön x-koordinaatti on = 0.
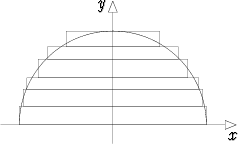
Keskiön y-koordinaatin laskemiseksi levy jaetaan periaatteessa pikku neliöihin
vastaten edellä käsiteltyjä pikku kuutioita, koska kyseessä on kaksiulotteinen
kappale. Näistä voidaan kuitenkin yhdistää ne, joita vastaa sama y-arvo, jolloin
levy tulee jaetuksi x-akselin suuntaisiin pitkiin ja kapeisiin suorakulmioihin, joiden
sivut ovat  yk ja 2
yk ja 2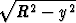 .
.
y-koordinaattien keskiarvoa approksimoidaan nyt painotettuna keskiarvona, jossa painoina ovat tällaisten suorakulmioiden alat:
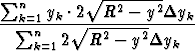 .
.
Jaon tihentäminen, so. suorakulmioiden kaventaminen ja lukumäärän lisääminen
johtaa sekä osoittajassa että nimittäjässä määrättyyn integraaliin. Nimittäjän
integraali esittää puoliympyrän alaa ja on siis = 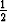
 R2. Keskiön y-koordinaatiksi
saadaan
R2. Keskiön y-koordinaatiksi
saadaan
Y0 = 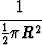 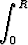 2y 2y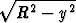 dy = dy = 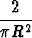 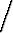 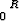 - - 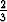 (R2 - y2)3/2 (R2 - y2)3/2 | ||||
= 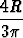 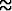 0.42R . 0.42R . |
![[#]](kuvat/msam10-c-4.gif) ympyrä ympyrä![[#]](kuvat/msam10-c-4.gif) koordinaatisto (xy-) koordinaatisto (xy-)![[#]](kuvat/msam10-c-4.gif) keskiarvo (painotettu) keskiarvo (painotettu)![[#]](kuvat/msam10-c-4.gif) määrätty integraali määrätty integraali![[#]](kuvat/msam10-c-4.gif) integrointi (kaavat) integrointi (kaavat)![[#]](kuvat/msam10-c-4.gif) integrointi (kaavat) integrointi (kaavat)![[#]](kuvat/msam10-c-4.gif) integrointi (sijoitus) integrointi (sijoitus)![[#]](kuvat/msam10-c-4.gif) integrointi
(osittais-) integrointi
(osittais-) |
Kivelä,  niinkuin matematiikka, versio 1.12
niinkuin matematiikka, versio 1.12