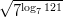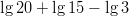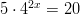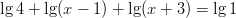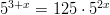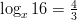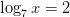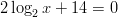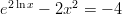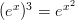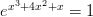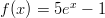Eksponentti- ja logaritmifunktiot

Eksponenttifunktio on paitsi matematiikassa myös matematiikan sovelluksissa eniten käytettyjä funktioita. Ehkä hieman yllättävää on, että se niinkin hyvin soveltuu monien fysikaalisten, kemiallisten, teknisten ym. ilmiöiden kuvaamiseen.
Eksponenttifunktioita on monia: kantaluku voi periaatteessa olla mikä tahansa positiiviluku ykköstä lukuunottamatta. Yleensä nimityksellä eksponenttifunktio tarkoitetaan tapausta, jossa kantalukuna on Neperin luku e = 2,71828… . Jos kantaluku on jokin muu, tästä mainitaan erikseen.
 Eksponenttifunktion määrittely ja perusominaisuudet
Eksponenttifunktion määrittely ja perusominaisuudet Yleisen eksponenttifunktion lausuminen Neperin luvun avulla
Yleisen eksponenttifunktion lausuminen Neperin luvun avulla Eksponenttifunktio sovelluksissa
Eksponenttifunktio sovelluksissa Neperin luvun määritelmä
Neperin luvun määritelmä
Kantaluvusta (≠1) riippumatta eksponenttifunktiolla on käänteisfunktio, jota kutsutaan logaritmifunktioksi. Jos kantalukuna on Neperin luku e, käytetään nimitystä luonnollinen logaritmi, lyhenteenä ln. Jos kantaluku on 10, kyseessä on Briggsin logaritmi, joka lyhennetään lg.
Logaritmifunktio ja erityisesti sen laskusäännöt tulevat käyttöön mallinnettaessa reaalimaailman ilmiöitä eksponenttifunktiolla (tai myös logaritmifunktiolla). Logaritmeilla on myös merkittävä historia: ennen elektronisten laskimien aikakautta (ts. ennen 1970-lukua) logaritmeja käytettiin helpottamaan moninumeroisia kerto- ja jakolaskuja.
 Logaritmifunktion määrittely
Logaritmifunktion määrittely Logaritmin laskusäännöt
Logaritmin laskusäännöt Eksponentti- ja logaritmiyhtälöt
Eksponentti- ja logaritmiyhtälöt Logaritmifunktion historiaa
Logaritmifunktion historiaa

Esimerkkejä
- Ratkaistaan yhtälö
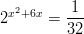 . Yhtälö voidaan myös
kirjoittaa muodossa
. Yhtälö voidaan myös
kirjoittaa muodossa
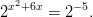
Nyt riittää, että ratkaisemme yhtälön
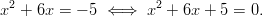
Ratkaisuksi saadaan

- Ratkaistaan yhtälö
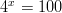 ottamalla ensin luonnollinen logaritmi
kummaltakin puolelta.
ottamalla ensin luonnollinen logaritmi
kummaltakin puolelta.
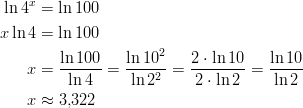
- Ratkaistaan yhtälö
 . Logaritmin
ääritelmän mukaan
. Logaritmin
ääritelmän mukaan 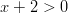 ja
ja  . Kumpikin ehto
toteutuu, kun
. Kumpikin ehto
toteutuu, kun 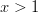 .
.

Otetaan kummastakin puolesta a-kantainen eksponenttifunktio.
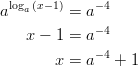
Ratkaisu toteuttaa vaatimuksen, kun
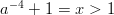 .
. 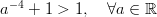 .
Lisäksi logaritmifunktiot ovat määriteltyjä vain, kun kanta
.
Lisäksi logaritmifunktiot ovat määriteltyjä vain, kun kanta 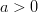 ja
ja
 . Yhtälön ratkaisu on siis
. Yhtälön ratkaisu on siis

- Exponentti- ja logaritmifunktioiden käänteisfunktiot.

Harjoitustehtäviä
- Laske:
-
- Ratkaise yhtälöt:
-
- Ratkaise yhtälöt:
-
- Sievennä:
-
- Määritä funktioiden nollakohdat:
-
Tehtävien vastaukset: