Funktion ominaisuudet

Derivaatan yksinkertaisimpia sovelluksia on funktion kulun tutkiminen: kasvavuus ja vähenevys, paikalliset ääriarvot, absoluuttiset suurimmat ja pienimmät arvot jossakin joukossa.
 Funktion kasvavuus ja vähenevyys; paikalliset ääriarvot
Funktion kasvavuus ja vähenevyys; paikalliset ääriarvot Ääriarvon laadun tutkiminen
Ääriarvon laadun tutkiminen Absoluuttinen maksimi ja minimi
Absoluuttinen maksimi ja minimi
Jos funktio f on kaikkialla derivoituva, sen derivaatat f'(x) kaikissa pisteissä x muodostavat uuden funktion f', joka mahdollisesti on edelleen derivoituva. Tällöin saadaan alkuperäisen funktion f toinen derivaatta f''. Tämäkin kertoo jotakin funktion ominaisuuksista: kuvaajan kuperuudesta ja kuperuuden vaihtumiskohdista, käännepisteistä.

Esimerkkejä
- Selvitetään milloin funktio
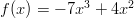 on kasvava
tarkastelemalla sen derivaatan merkkiä.
on kasvava
tarkastelemalla sen derivaatan merkkiä.

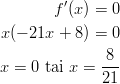
Funktio on kasvava, kun sen derivaattafunktio saa positiivisia arvoja.

Funktio on siis kasvava välillä
![-8 [0,21]](funktom4x.gif) .
. 
- Tutkitaan funktion
 ääriarvoja, kun
ääriarvoja, kun
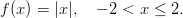
Funktiolla ei ole derivaatan nollakohtaa, sillä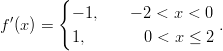
Ääriarvoja siis voi löytyä derivaatan epäjatkuvuuskohdasta
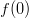 sekä välin päätepisteestä
sekä välin päätepisteestä 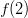 , jos
, jos 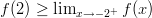 . Funktio
saa pienimmän arvonsa kohdassa
. Funktio
saa pienimmän arvonsa kohdassa  sekä suurimman arvonsa
kohdassa
sekä suurimman arvonsa
kohdassa 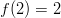 , jos
, jos 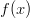 olisi määritelty välillä
olisi määritelty välillä  saisi se suurimman arvonsa kohdissa
saisi se suurimman arvonsa kohdissa 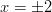 .
. 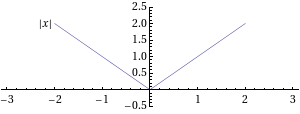
- Tutkitaan funktion
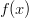 ääriarvoja, kun
ääriarvoja, kun

Funktiolla ei ole derivaatan nollakohtaa, sillä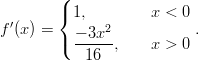
Funktion epäjatkuvuuskohdassakaan funktio ei saa suurinta arvoaan, sillä
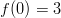 ja
ja  .
.
Funktio ei saa myöskään pienintä arvoa, koska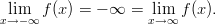
Funktiolla on suurin yläraja
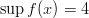 .
.
- Tutkitaan polynomifunktion
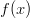 luonnetta, kun
luonnetta, kun
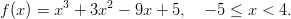
Funktio on jatkuva ja derivoituva. Ääriarvoja voidaan löytää funktion derivaatan nollakohdista tai välin päätepisteestä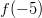 .
.
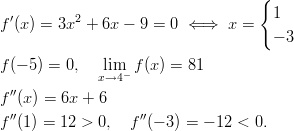
Funktiolla on siis lokaalit minimit kohdassa
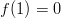 ja
ja  ja
koska funktio ei saa pienempiä arvoja, ovat ne samalla globaalit minimit.
Funktiolla on lokaali maksimi kohdassa
ja
koska funktio ei saa pienempiä arvoja, ovat ne samalla globaalit minimit.
Funktiolla on lokaali maksimi kohdassa 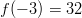 . Funktiolla ei ole
kuitenkaan globaalia maksimia, sillä
. Funktiolla ei ole
kuitenkaan globaalia maksimia, sillä

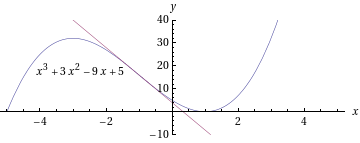
Funktiolla on käännepiste, kun
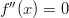 ja
ja  vaihtaa merkkiä
tuon pisteen ympäristössä. Jos
vaihtaa merkkiä
tuon pisteen ympäristössä. Jos 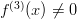 tuossa pisteessä, niin
kyseinen piste on varmasti funktion käännepiste.
tuossa pisteessä, niin
kyseinen piste on varmasti funktion käännepiste.
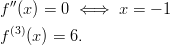
Funktiolla on siis käännekohta kohdassa
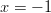 , sillä
, sillä 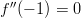 ja
ja
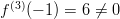 .
. 
- ääriarvojen tutkimista voidaan soveltaa esimerkiksi geometrisiin
ongelmiin.
 Esimerkki 1 maksimin ja minimin laskemisesta
Esimerkki 1 maksimin ja minimin laskemisesta

Harjoitustehtäviä
- Määritä funktion
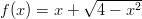 suurin ja pienin arvo.
suurin ja pienin arvo.
- Millä
 :n arvoilla funktio
:n arvoilla funktio 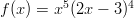 on aidosti kasvava?
on aidosti kasvava?
- Osoita, että yhtälöllä
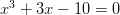 on täsmälleen yksi
reaalinen ratkaisu.
on täsmälleen yksi
reaalinen ratkaisu.
- Määritä funktion
 huipun
koordinaatit, kun
huipun
koordinaatit, kun 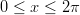 .
.
- Millä vakion
 arvoilla funktio
arvoilla funktio  on
kaikkialla kasvava?
on
kaikkialla kasvava?
- Pallo heitetään suoraan ylöspäin 15 metriä korkean talon katolta
nopeudella 22 m/s. Sen korkeus maan pinnalta metreinä saadaan silloin
yhtälöstä
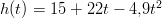 , jossa
, jossa 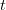 on heitosta kulunut aika
sekunteina.
on heitosta kulunut aika
sekunteina.
- Määritä Pallon nopeus ja kiihtyvyys, kun heitosta on
kulunut yksi sekunti.
- Alas tullessaan pallo ohittaa täpärästi katon ja putoaa
maahan. Kuinka kauan pallo oli ilmassa?
- Määritä Pallon nopeus ja kiihtyvyys, kun heitosta on
kulunut yksi sekunti.
- Etsi funktion
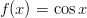 käännepisteet ja niitä vastaavat
tangenttisuorat.
käännepisteet ja niitä vastaavat
tangenttisuorat.
Tehtävien vastaukset:
