| Sanna Ranto, LUKUTEORIA JA ALGEBRA Versio 1, 1.11.2003 | KUNTA |
Maksimaalinen ihanne
Kommutatiivisista renkaista voidaan muodostaa kuntia maksimaalisen ihanteen avulla.
Määritelmä. Olkoon (R, +, . ) rengas. Renkaan R ihannetta M sanotaan maksimaaliseksi,
jos se on aito (toisin sanoen M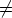 R) ja ei ole olemassa renkaan R ihannetta I, joka toteuttaisi
M
R) ja ei ole olemassa renkaan R ihannetta I, joka toteuttaisi
M  I
I  R.
R.
Määritelmän jälkimmäinen ehto on usein mukava ajatella muodossa: Jos I on renkaan
(R, +, . ) ihanne ja M  I, niin I = R.
I, niin I = R.
Lause. Olkoon (R, +, . ) kommutatiivinen rengas ja I sen ihanne. Jäännösluokkarengas (R/I, +, . ) on kunta jos ja vain jos I on renkaan (R, +, . ) maksimaalinen ihanne.
Todistus. Oletetaan ensin, että (R/I, +, . ) on kunta. Koska kunnassa on vähintään kaksi
alkiota, niin I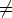 R. Oletetaan, että on olemassa renkaan (R, +, . ) ihanne J, jolle pätee I
R. Oletetaan, että on olemassa renkaan (R, +, . ) ihanne J, jolle pätee I  J.
Näytetään, että tästä seuraa J = R.
J.
Näytetään, että tästä seuraa J = R.
Koska I on ihanteen J aito osajoukko, on olemassa alkio a  J \I. Silloin a + I
J \I. Silloin a + I I, joten a + I
ei ole kunnan (R/I, +, . ) nolla-alkio. Täten alkiolla a + I on käänteisalkio b + I jollakin b
I, joten a + I
ei ole kunnan (R/I, +, . ) nolla-alkio. Täten alkiolla a + I on käänteisalkio b + I jollakin b  R,
siis
R,
siis
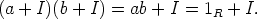
Tästä saadaan, että 1R = ab + i, jollain alkiolla i  I. Koska a
I. Koska a  J ja i
J ja i  J, niin
ab + i
J, niin
ab + i  J ehdon I2 nojalla. Kuten sivulla Ihanne todettiin siitä, että 1R
J ehdon I2 nojalla. Kuten sivulla Ihanne todettiin siitä, että 1R  J seuraa, että
J = R.
J seuraa, että
J = R.
Todistetaan väite toiseen suuntaan eli oletetaan, että I on renkaan R maksimaalinen ihanne. Koska rengas R on kommutatiivinen, niin samoin on jäännösluokkarengas (R/I, +, . ). Vielä pitää osoittaa, että kaikilla jäännösluokkarenkaan (R/I, +, . ) nolla-alkiosta I eroavilla alkioilla on käänteisalkio joukossa R/I.
Olkoon a + I  R/I erisuuri kuin I. Silloin a /
R/I erisuuri kuin I. Silloin a / I. Koska I on maksimaalinen ihanne, niin
joukon {I,a} generoima ihanne on oltava R. Koska (R/I, +, . ) on kommutatiivinen, saadaan
sivun Ihanteen generointi ja pääihannerengas lauseen mukaan, että
I. Koska I on maksimaalinen ihanne, niin
joukon {I,a} generoima ihanne on oltava R. Koska (R/I, +, . ) on kommutatiivinen, saadaan
sivun Ihanteen generointi ja pääihannerengas lauseen mukaan, että
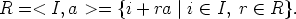
Koska kaikki joukon R alkiot voidaan esittää muodossa i + ra, niin erityisesti ykkösalkio
1R = i' + r'a, joillakin i' I ja r'
I ja r' R. Tämä on ekvivalenttia sen kanssa, että
R. Tämä on ekvivalenttia sen kanssa, että
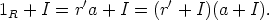
Täten r' + I on alkion a + I käänteialkio ja (R/I, +, . ) on siis kunta. ![[]](images/msam10-c-3.gif)
Linkit:
Rengas
Kunta
Ihanne
Jäännösluokkarengas
Ihanteen generointi ja pääihannerengas