Sisällön pääryhmät Todennäköisyys Tilastomatematiikka [ 1 2 3 4 5 6 7 8 ] ESITIEDOT: KATSO MYÖS:  todennäköisyyslaskenta,  todennäköisyysjakaumat,  keskiarvo

Kansisivu  Sisältö  Hakemisto

Korrelaatiokerrointa laskettaessa kumpikin data ensin skaalataan sen keskiarvolla ja keskihajonnalla, minkä jälkeen muodostetaan parittainen tulosumma:

r =  .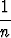

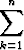
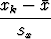
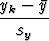Täss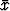ä ja 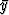tarkoittavat kummastakin datasta laskettuja keskiarvoja, s_x ja s_y ovat vastaavasti keskihajonnat. Lauseke voidaan saattaa myös muotoon

r = ,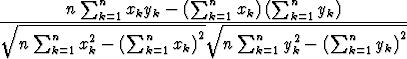

jolloin tarvitsee laskea datasta vain summat, neliösummat ja tulosumma.

Korrelaatiokerroin on aina välillä [-1, 1]. Sen merkin mukaan puhutaan positiivisesta tai negatiivisesta korrelaatiosta. Mitä lähempänä ykköstä arvo on, sitä vahvempaa on ominaisuuksien esiintyminen yhdessä. Lähellä arvoa -1 oleva korrelaatiokerroin osoittaa vastaavasti, että ominaisuudet eivät yleensä esiinny samanaikaisesti.

Vahvan positiivisen korrelaation sanotaan usein tarkoittavan ominaisuuksien välistä riippuvuutta. Tästä ei kuitenkaan voida päätellä, että ominaisuuksien välillä olisi kausaalisuhde, ts. toinen olisi toisen syy. Kyse on vain siitä, että ominaisuudet käyttäytyvät samansuuntaisesti. Niillä saattaa esimerkiksi olla jokin kolmas ominaisuus yhteisenä syynä.

Kun korrelaatiokerroin lasketaan otoksesta, joudutaan erikseen miettimään sen merkitsevyyttä. Otoksen epäedustavuus tai pienuus saattaa johtaa siihen, että esimerkiksi korrelaatiokertoimen arvon |r| < 0.5 ei voida katsoa merkitsevästi poikkeavan nollasta.

Edellä olevassa Teknillisen korkeakoulun matematiikan peruskurssin välikokeita koskevassa esimerkissä välikoemenestysten välinen korrelaatiokerroin on 0.61.

summamerkintä

Kivelä, niinkuin matematiikka, versio 1.12