Todennäköisyyslaskennan peruskäsitteet
Todennäköisyyslaskennassa tarkastelun kohteena ovat satunnaisilmiöt.
Esimerkkejä tällaisista ovat tavallisen kuusitahkoisen nopan heitto ja vaikkapa
tikan heitto tauluun.
Kaikki ilmiön mahdolliset tulokset muodostavat joukon 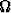 , jota kutsutaan
otosavaruudeksi. Nopan tapauksessa tämä on joukko {1, 2, 3, 4, 5, 6} vastaten
heiton tuloksena saatavia silmälukuja. Tikanheitossa tulokset ovat sopivassa
koordinaatistossa ilmoitettuja koordinaattipareja (x, y), jotka ilmaisevat, mihin
pisteeseen tikka osuu. Luontevaa on valita tikkataulun keskipiste origoksi ja
yksiköksi senttimetri. Otosavaruudeksi voidaan tällöin ottaa xy-taso, vaikka kaikki
sen pisteet eivät varmasti olekaan mahdollisia heittotuloksia.
, jota kutsutaan
otosavaruudeksi. Nopan tapauksessa tämä on joukko {1, 2, 3, 4, 5, 6} vastaten
heiton tuloksena saatavia silmälukuja. Tikanheitossa tulokset ovat sopivassa
koordinaatistossa ilmoitettuja koordinaattipareja (x, y), jotka ilmaisevat, mihin
pisteeseen tikka osuu. Luontevaa on valita tikkataulun keskipiste origoksi ja
yksiköksi senttimetri. Otosavaruudeksi voidaan tällöin ottaa xy-taso, vaikka kaikki
sen pisteet eivät varmasti olekaan mahdollisia heittotuloksia.
Otosavaruuden alkioita kutsutaan alkeistapauksiksi.
Tapahtumalla tarkoitetaan otosavaruuden 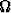 osajoukkoa. Nopanheitossa se voi olla
esimerkiksi tulos ’vähintään 3’, ts. joukko {3, 4, 5, 6}; tikanheitossa ’alle 5
senttimetrin päähän keskipisteestä’ eli {(x, y) | x2 + y2 < 25}.
osajoukkoa. Nopanheitossa se voi olla
esimerkiksi tulos ’vähintään 3’, ts. joukko {3, 4, 5, 6}; tikanheitossa ’alle 5
senttimetrin päähän keskipisteestä’ eli {(x, y) | x2 + y2 < 25}.
Jokaiseen tapahtumaan liitetään todennäköisyys P , so. funktio, jonka argumentteina
ovat em. osajoukot. Tällä tulee olla seuraavat ominaisuudet:
- 0 < P (A) < 1, olipa A mikä tahansa tapahtuma.
- P (
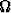 ) = 1 eli ns. varman tapahtuman todennäköisyys on = 1.
) = 1 eli ns. varman tapahtuman todennäköisyys on = 1.
- P (A
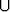 B) = P (A) + P (B), jos A
B) = P (A) + P (B), jos A 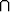 B = Ø, ts. jos A ja B ovat erillisiä.
B = Ø, ts. jos A ja B ovat erillisiä.
Funktio P kuvaa tapahtuman todennäköisyyttä: mitä lähempänä P (A) on arvoa
1, sitä todennäköisempi on tapahtuma A.
Eo. ominaisuuksien seurauksena on mm. komplementtitapahtuman 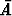 =
= 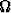 \ A
todennäköisyyttä koskeva sääntö: Koska P (A) + P (
\ A
todennäköisyyttä koskeva sääntö: Koska P (A) + P (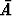 ) = P (A
) = P (A 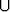
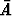 ) = P (
) = P (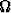 ) = 1,
on P (
) = 1,
on P (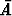 ) = 1 - P (A). (Todennäköisyyslaskennassa käytetään yleensä merkintää
) = 1 - P (A). (Todennäköisyyslaskennassa käytetään yleensä merkintää 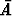 joukko-opillisen komplementin merkinnän
joukko-opillisen komplementin merkinnän 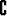 A sijasta.)
A sijasta.)
Eo. ominaisuudet eivät määrää funktiota P , vaan ainoastaan asettavat sille tietyt
järkevyysvaatimukset. Funktion määrittäminen kussakin yksityistapauksessa
edellyttää jotakin lisätietoa ilmiöstä.
Hieman täsmällisempään muotoon kirjoitettuina funktiolta P vaadittavia
ominaisuuksia kutsutaan Kolmogorovin aksioomiksi todennäköisyyslaskennan
perusteita tutkineen neuvostoliittolaisen matemaatikon Andrei Nikolajevitš
Kolmogorovin (1903 – 1987) mukaan.
Kivelä,  niinkuin matematiikka, versio 1.12
niinkuin matematiikka, versio 1.12
![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät
Sisällön pääryhmät  Todennäköisyys
Todennäköisyys  Todennäköisyyslaskenta [
1 2 3 4 5 6 7 ]
Todennäköisyyslaskenta [
1 2 3 4 5 6 7 ]
![[#]](kuvat/msam10-c-4.gif) joukko-oppi,
joukko-oppi, ![[#]](kuvat/msam10-c-4.gif) lukumäärän laskeminen,
lukumäärän laskeminen, ![[#]](kuvat/msam10-c-4.gif) funktiokäsite
funktiokäsite
![[#]](kuvat/msam10-c-4.gif) tilastomatematiikka,
tilastomatematiikka, ![[#]](kuvat/msam10-c-4.gif) todennäköisyysjakaumat
todennäköisyysjakaumat
![[#]](kuvat/msam10-c-4.gif) Kansisivu
Kansisivu
![[#]](kuvat/msam10-c-4.gif) Sisältö
Sisältö
![[#]](kuvat/msam10-c-4.gif) Hakemisto
Hakemisto
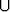
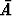
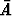
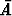
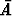 joukko-opillisen komplementin merkinnän
joukko-opillisen komplementin merkinnän