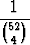Esimerkkejä kombinatorisesta todennäköisyyslaskennasta
Mikäli alkeistapauksia on äärellinen määrä ja on perusteltua pitää näitä yhtä
todennäköisinä, johtaa todennäköisyyksien laskeminen usein erilaisten
kombinaatioiden lukumäärien laskemiseen.
1) Arpajaisissa on 100 arpaa, joista kymmenen on voittoarpoja. Henkilö ostaa
viisi arpaa. Millä todennäköisyydellä hän saa ainakin yhden voiton?
Alkeistapauksia olkoot 100 arvan joukosta poimitut viiden arvan kombinaatiot.
Näitä on kaikkiaan 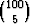 = 75287520. Kombinaatioita on perusteltua pitää
yhtä todennäköisinä, jolloin tietyn kombinaation todennäköisyys on
1/
= 75287520. Kombinaatioita on perusteltua pitää
yhtä todennäköisinä, jolloin tietyn kombinaation todennäköisyys on
1/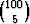 = 1/75287520.
= 1/75287520.
Tapahtuma, jonka todennäköisyyttä kysytään, on A = ’ainakin yksi voitto’.
Tämän komplementtitapahtuma on 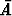 = ’ei yhtään voittoa’. Tapahtumaan
= ’ei yhtään voittoa’. Tapahtumaan 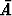 kuuluvia kombinaatioita on
kuuluvia kombinaatioita on 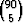 = 43949268 kappaletta ja siis
= 43949268 kappaletta ja siis
P (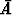 ) = 43949268 .
) = 43949268 . 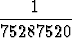
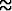 0.584.
0.584.
Todennäköisyys saada ainakin yksi voitto on siis P (A) = 1 - P (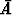 )
) 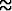 0.416.
0.416.
2) Hyvin sekoitetusta korttipakasta vedetään neljä korttia. Millä todennäköisyydellä
ne ovat eri maita?
Keskenään yhtä todennäköisiä alkeistapauksia ovat 52 kortin pakasta otetut
neljän kortin kombinaatiot, joiden lukumäärä on 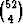 . Jokaisen kombinaation
todennäköisyys on siis 1/
. Jokaisen kombinaation
todennäköisyys on siis 1/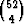 . Eri maita olevien kombinaatioiden määrä on 134,
koska jokaisesta maasta kortti voidaan valita 13 tavalla. Todennäköisyys on
siten
. Eri maita olevien kombinaatioiden määrä on 134,
koska jokaisesta maasta kortti voidaan valita 13 tavalla. Todennäköisyys on
siten
134 . 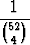
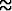 0.105.
0.105.
Kivelä,  niinkuin matematiikka, versio 1.12
niinkuin matematiikka, versio 1.12
![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät
Sisällön pääryhmät  Todennäköisyys
Todennäköisyys  Todennäköisyyslaskenta [
1 2 3 4 5 6 7 ]
Todennäköisyyslaskenta [
1 2 3 4 5 6 7 ]
![[#]](kuvat/msam10-c-4.gif) joukko-oppi,
joukko-oppi, ![[#]](kuvat/msam10-c-4.gif) lukumäärän laskeminen,
lukumäärän laskeminen, ![[#]](kuvat/msam10-c-4.gif) funktiokäsite
funktiokäsite
![[#]](kuvat/msam10-c-4.gif) tilastomatematiikka,
tilastomatematiikka, ![[#]](kuvat/msam10-c-4.gif) todennäköisyysjakaumat
todennäköisyysjakaumat
![[#]](kuvat/msam10-c-4.gif) Kansisivu
Kansisivu
![[#]](kuvat/msam10-c-4.gif) Sisältö
Sisältö
![[#]](kuvat/msam10-c-4.gif) Hakemisto
Hakemisto
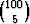
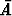
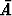 kuuluvia kombinaatioita on
kuuluvia kombinaatioita on 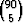
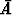
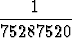
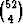 . Jokaisen kombinaation
todennäköisyys on siis
. Jokaisen kombinaation
todennäköisyys on siis 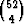 . Eri maita olevien kombinaatioiden määrä on
. Eri maita olevien kombinaatioiden määrä on