![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät
Sisällön pääryhmät  Diskreettiä matematiikkaa
Diskreettiä matematiikkaa  Lukumäärän
laskeminen [ 1 2 3 4 5 6 7 ]
Lukumäärän
laskeminen [ 1 2 3 4 5 6 7 ]
ESITIEDOT:
KATSO MYÖS:
![[#]](kuvat/msam10-c-4.gif) joukko-oppi,
joukko-oppi, ![[#]](kuvat/msam10-c-4.gif) binomi- ja multinomikertoimet
binomi- ja multinomikertoimet
![[#]](kuvat/msam10-c-4.gif) Kansisivu Kansisivu
![[#]](kuvat/msam10-c-4.gif) Sisältö Sisältö
![[#]](kuvat/msam10-c-4.gif) Hakemisto Hakemisto |
![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät Sisällön pääryhmät  Diskreettiä matematiikkaa Diskreettiä matematiikkaa  Lukumäärän
laskeminen [ 1 2 3 4 5 6 7 ] Lukumäärän
laskeminen [ 1 2 3 4 5 6 7 ]
ESITIEDOT: KATSO MYÖS: ![[#]](kuvat/msam10-c-4.gif) joukko-oppi, joukko-oppi, ![[#]](kuvat/msam10-c-4.gif) binomi- ja multinomikertoimet binomi- ja multinomikertoimet
|
|
Olkoon annettuna n kappaletta merkkejä (olioita, alkioita)
a1, a2, a3, ..., an.
Tehtävänä on selvittää, monellako tavalla näistä voidaan poimia p kappaletta, kun huomiota ei kiinnitetä poimittavien merkkien keskinäiseen järjestykseen. Sama voidaan lausua toisin: Montako p alkion muodostamaa osajoukkoa joukolla {a1, a2, a3, ..., an} on?
Poimittavia p merkin yhdelmiä kutsutaan p-kombinaatioiksi.
Jos poimittavien merkkien keskinäinen järjestys otetaan huomioon, on kyseessä p-variaatioiden lukumäärä. Variaatioita on n!/(n - p)! kappaletta. Näiden joukossa on kuitenkin sellaisia, joissa on samat merkit, mutta eri järjestyksissä. Koska tietyt p merkkiä voidaan järjestää p! järjestykseen, on samat merkit sisältäviä järjestyksiä aina p! kappaletta, jolloin p-kombinaatioiden määrä saadaan jakamalla p-variaatioiden määrä luvulla p!. Lukumäärä on siis
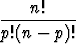 .
.
Tätä kutsutaan myös binomikertoimeksi ja merkitään 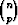 .
.
Siis:
n alkion joukosta voidaan valita p kappaletta 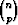 eri tavalla, kun järjestykseen ei
kiinnitetä huomiota.
eri tavalla, kun järjestykseen ei
kiinnitetä huomiota.
Esimerkiksi merkeistä a, b, c, d voidaan poimia kahden merkin yhdelmiä 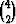 = 6
kappaletta. Nämä ovat
= 6
kappaletta. Nämä ovat
ab, ac, ad, bc, bd, cd.
Koska p-kombinaatiot ovat p-alkioisia osajoukkoja, tulee näiden lukumäärien summan olla sama kuin kaikkien osajoukkojen lukumäärä, kun huomioon otetaan kaikki mahdolliset arvot p, ts. p = 0, 1, ..., n. On siis oltava
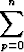
 = 2n.
= 2n.
Tämä on erikoistapaus binomikaavasta (x + y)n = 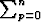
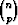 xn-pyp, kun asetetaan
x = y = 1.
xn-pyp, kun asetetaan
x = y = 1.
![[#]](kuvat/msam10-c-4.gif) osajoukko osajoukko![[#]](kuvat/msam10-c-4.gif) joukko joukko![[#]](kuvat/msam10-c-4.gif) binomikerroin binomikerroin![[#]](kuvat/msam10-c-4.gif) binomikerroin binomikerroin![[#]](kuvat/msam10-c-4.gif) summamerkintä summamerkintä![[#]](kuvat/msam10-c-4.gif) binomikaava binomikaava![[#]](kuvat/msam10-c-4.gif) binomikaava binomikaava |
Kivelä,  niinkuin matematiikka, versio 1.12
niinkuin matematiikka, versio 1.12