![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät
Sisällön pääryhmät  Diskreettiä matematiikkaa
Diskreettiä matematiikkaa  Lukumäärän
laskeminen [ 1 2 3 4 5 6 7 ]
Lukumäärän
laskeminen [ 1 2 3 4 5 6 7 ]
ESITIEDOT:
KATSO MYÖS:
![[#]](kuvat/msam10-c-4.gif) joukko-oppi,
joukko-oppi, ![[#]](kuvat/msam10-c-4.gif) binomi- ja multinomikertoimet
binomi- ja multinomikertoimet
![[#]](kuvat/msam10-c-4.gif) Kansisivu Kansisivu
![[#]](kuvat/msam10-c-4.gif) Sisältö Sisältö
![[#]](kuvat/msam10-c-4.gif) Hakemisto Hakemisto |
![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät Sisällön pääryhmät  Diskreettiä matematiikkaa Diskreettiä matematiikkaa  Lukumäärän
laskeminen [ 1 2 3 4 5 6 7 ] Lukumäärän
laskeminen [ 1 2 3 4 5 6 7 ]
ESITIEDOT: KATSO MYÖS: ![[#]](kuvat/msam10-c-4.gif) joukko-oppi, joukko-oppi, ![[#]](kuvat/msam10-c-4.gif) binomi- ja multinomikertoimet binomi- ja multinomikertoimet
|
|
Olkoon annettuna n kappaletta merkkejä (olioita, alkioita)
a1, a2, a3, ..., an,
joista on kaikilla mahdollisilla tavoilla poimittava p kappaletta ja esitettävä nämä kaikissa mahdollisissa järjestyksissä. Näitä kutsutaan toisinaan merkkien p-variaatioiksi.
Ensimmäinen merkki voidaan valita n eri tavalla, koska kaikki merkit ovat käytettävissä. Seuraava on valittava jäljellä olevista n - 1 merkistä, joten mahdollisuuksia on n - 1. Kolmatta merkkiä valittaessa mahdollisuuksia on n - 2. Kun näin jatketaan, on viimeiselle eli p:nnelle merkille n - p + 1 valintamahdollisuutta.
Mahdollisuuksia on kaikkiaan
n . (n - 1) . ... . (n - p + 1) = 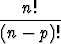 .
.
Siis:
n merkin p-variaatioiden lukumäärä on n!/(n - p)!.
Esimerkiksi merkeistä a, b, c, d voidaan poimia kahden merkin järjestettyjä jonoja 4!/(4 - 2)! = 12 kappaletta. Nämä ovat
| ab, | ac, | ad, | ba, | bc, | bd, | ||||||||||||||||||
| ca, | cb, | cd, | da, | db, | dc. |
![[#]](kuvat/msam10-c-4.gif) kertoma kertoma |
Kivelä,  niinkuin matematiikka, versio 1.12
niinkuin matematiikka, versio 1.12